2192973026

Często liczby zespolone będziemy zapisywali w postaci a + ib. Tak więc liczbę 2 równą a + ib możemy przedstawić w postaci

z = re z + i • im z.

Liczbę zespoloną, mającą postać yi, gdzie (rzecz jasna) y jest liczbą rzeczywistą, nazywamy liczbą czysto urojoną.

Jeśli z = x + iy, to liczbę z, mającą postać

z = x — iy,

nazywamy liczbą sprzężoną do liczby z.

Twierdzenie 2 Dla dowolnych liczb zespolonych Z\, z₂ spełnione są warunki:

Z\ + z₂ = zi + z₂,

Z\ — z₂ — Z\ — z₂,

zi ■ z₂ = zi ■ z₂,

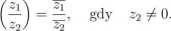
Przykład 1 Oto kilka przykładów działań na liczbach zespolonych.

(1 +1) + (2 — 5*) = 3 —4ś,

(2 + 3i) • (4 - 6*) = 8 - 12ż + 12« + 18 = 26,

3 + 2 i (3 + 2z)(l — i) 3 + 2-3i + 2i 5    1 .

1 + i ~ (1 + *)(1 —i) ^_    2    " 2 ^_ 2 ' *'

Przykład 2 Przykłady wyznaczania części rzeczywistej i urojonej.

re (—3 + 4i) = —3, im(—3 + 4ż) = 4, re (3 - 7i) = 3, im (3 - 7i) = -7,

(21 + 13*) = 21 - 13 i, (21 - 13«) = 21 + 13*.

5