2659241288

Wykład 5

30.10.2007

Niech r będzie liczbą naturalną większą od 1, d liczbą naturalną, G dowolnym niepustym podzbiorem R¹', zaś p będzie punktem z R^r.

Pochodna kierunkowa

Uwaga 5.1 Pochodne cząstkowe można uogólnić otrzymując tzw. pochodne kierunkowe.

Definicja 5.1 Niech v będzie wektorem niezerourym z R^r, G zbiorem otwartym w £^r, p punktem tego zbioru, a f: G —* R dowolną funkcją.

Pochodną kierunkową funkcji f w punkcie p w kierunku wektora v nazywamy granicę

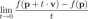
o ile ta granica istnieje. Oznaczamy ją symbolem f^(p).

Wniosek 5.1 Niech G zbiorem otwartym w £^r. p punktem tego zbioru, a f : G —* R dowolną funkcją.

Pochodna cząstkowa rzędu pierwszego względem zmiennej x,- w punkcie p funkcji f jest pochodną kierunkową funkcji f w punkcie p w kierunku wektora e,-, o ile taka pochodna cząstkowa istnieje.

Uwaga 5.2 Zauważmy, że można też mówić o pochodnej kierunkowej w kierunku wektora v w punkcie p dla odwzorowania f:G—> R^d. Otrzymujemy wtedy wektor z R^rf, którego składowymi są pochodne kierunkowe składowych odwzorowania f w kierunku wektora v w punkcie p.

Uwaga 5.3 Również warunek konieczny dla różniczkowalności można wyrazić za pomocą pochodnych kierunkowych.

Twierdzenie 5.1 Niech G będzie zbiorem otwartym w £^T, p punktem zG, f: G —• M dowolną funkcją.

Jeżeli funkcja f jest różniczkowalna w punkcie p, to dla dowolnego dowolnego niezerowego wektora v € R^r pochodna kierunkowa funkcji f w punkcie p w kierunku wektora v istnieje oraz zachodzi równość

/v(P) = /'(P)v-

Definicja 5.2 Niech G będzie zbiorem otwartym w £', a punkt p punktem tego zbioru, f:G—> R dowolną funkcją.

Jeśli f jest funkcją różniczkowalną w p, to gradientem funkcji f w punkcie p nazywamy taki wektor z R^r oznaczany grad /(p), że dla każdego wektora h 6 R^r zachodzi równość

/'(p)h = (grad/(p)|h).

Uwaga 5.4 Gradient funkcji f w punkcie p oznacza się również V/(p).

Uwaga 5.5 Zauważmy, żt

v/(p) - [

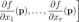
17