3754969723

9

1.2. PODSTAWOWE WŁASNOŚCI, WZORY FRENETA

Stosujemy teraz wyliczoną wcześniej postać ei(s + As):

cos A</?ei(s) + sin Aipe2(s) — e\(s) As

Aip — 1 . .    sin Aip . ,

■A^^{ei(s) +} A^hS^^^e2(s)

cos Aip — 1

(.

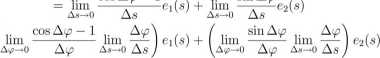
= 0 ■ e,(s) + ir_c(c(s))e₂(s)

Mamy więc:

co daje:

{c",e i) = (K_ce₂,e₂) = K_c,

|c"|² = <c",c") = K%(e₂, e₂) = Kl

W ten sposób udowodniliśmy punkt 2. Przechodzimy do dowodu punktu 3. Wektory ei,e2 stanowią bazę, więc wektor e* możemy zapisać w tej bazie:

it(t) = TOii (t)e,(t) + w_i2 (t)e₂(t)

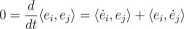
Podstawimy teraz do powyższego wzoru, e.\ przedstawione w bazie ei,e2: 0 = (-wnei + WU&2, e-z) + (ei, W2iei, W22^) =    + W2\

Podobnie wyliczamy ^(ei,ei):

0 = (ći,ei) + (ei, ći) = Wn + Wn — 0

Z powyższych rozważań wynika, że:

w₂i = -w 12

Wn = W22 = 0

Co daje nam:

ei = u>i₂e₂ e₂ = -w_nei

Z wcześniej udowodnionych własności wynika, że Ł\ = c = /ć_ce₂ = W\₂e₂, czyli W12 = K_c.    □