6324061395

Krzywe stożkowe

Krzywą stożkową w prostokątnym kartezjańskim układzie współrzędnych zapisujemy jako:

Ax² + Bxy + Cy² + Dx + Ey + F = 0, przy czym A,B i C nie mogą być jednocześnie równe 0.

Koło: A = C, B = 0,

Elipsa: B² - 4AC < 0,

Parabola: B² - 4AC = 0,

Hiperbola: B² - 4AC > 0.

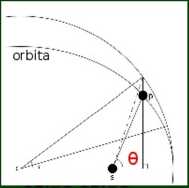
W układzie biegunowym (r,0) ogólne równanie krzywej stożkowej przyjmuje postać:

P

r = -

1 + e cos 0

Kąt 0 nazywany jest anomalią prawdziwą, e jest mimośrodem. Parametr p związany jest z mimośrodem i wielką półosią a równaniem: p = a (1 - e²)