7581047565

KAPITAŁ LUDZKI

NARODOWA STRATEGIA SPÓJNOŚCI

UNIA EUROPEJSKA

EUROPEJSKI FUNDUSZ SPOŁECZNY

Temat 5. Wybrane zagadnienia układu sił przestrzennych 5.1. Moment siły względem osi

Rozważmy siłę F w ogólności skośną względem pewnej osi 1.

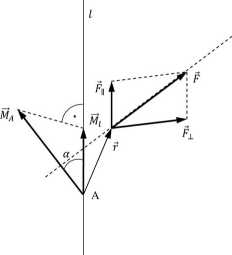
•    Rozłóżmy siłę F na dwie składowe: F|| i F_±; Moment względem osi / ma jedynie składowa F_±.

•    Wyznaczmy moment M_A siły F względem dowolnego punktu A leżącego na osi /

M_A = f x F

•    Zrzutuj my prostokątnie M_A na oś /.

•    Można udowodnić, że rzut ten jest momentem Mi siły F_± względem osi /, czyli momentem siły F względem osi /. Stąd

Mi — | M_a | cos a

Można sformułować następujące twierdzenie:

„Momentem siły względem osi jest rzut na tę oś wektora momentu tejże siły, wyznaczonego względem dowolnego punktu tej osi”.

Literatura: |2] rozdz. 7.6. str. 152-^155.

5.2. Warunki równowagi statycznej przestrzennego układu sił.

Dowolny układ sił, podobnie jak układ płaski, można zawsze zredukować w dowolnym punkcie do wektora głównego W_g i momentu głównego M_g. Aby układ był w równowadze statycznej, oba wektory muszą być jednocześnie zero.

Stąd warunki ogólne (inaczej wektorowe)

Wg = 0 Mg = 0

Nie istnieją oczy wiście, jak w przypadku płaskiego układu sił, warunki wykreślne (graficzne).

Warunki analityczne (inaczej warunki równowagi statycznej) są układem sześciu równań. Pierwsze trzy warunkują zerowanie się składowych wektora głównego na osiach układu OXYZ, natomiast trzy kolejne zerowanie się rzutów wektora momentu głównego na osie układu OXYZ, czyli momentów sił układu względem osi układu OXYZ

Projekt „Rozwój i promocja kierunków technicznych w Akademii Morskiej w Szczecinie” Akademia Morska w Szczecinie, ul. Wały Chrobrego 1-2, 70-500 Szczecin