8839840529

Egzamin No. 1 poprawkowy, 24.2’96

1. Obliczyć lim n( — l), jeśli a_n := n^p logn, gdzie p G Rjest ustalone.

2. Obliczyć granicę funkcji w punkcie:

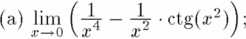
(b) lim

x—>-0

e* - ą/1 + 2x log(cos x)

3.    Dowieść, że G R zachodzi nierówność 1 4* §log(a? -f \/l + x²) ^    +

4.    Zbadać przebieg i naszkicować wykres funkcji /:R\{1}—iR, /(a?) := (x + 1) exp _x_^-

5. Zbadać zbieżność i bezwzględną zbieżność szeregów:

oo

(^a) E

n=2

\/5- 1. logn ’

oo

(b) E(-ir

n=l

n + 1    _ i

Vn² + 100

6. Obliczyć całki nieoznaczone:

(a)

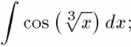
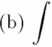
t²dt

(t²+t + l)²