8903649753

U\

Ul

Rys. 9. Schemat ideowy rozważanego obwodu prądu przemiennego

/ = 4e^lSU A,	(12)
U, = 5,64 e‘^j8l° V,	(13)
U2= 20,4 e*^25'^6” V,	04)
U3 = 8,92 e‘^jll6'^6° V.	(15)

stanowią prądy i napięcia zespolone poszczególnych gałęzi oraz impedancjc zastępcze.

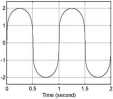
Rys. 7. Przebieg wartości chw ilowych symulowanego prądu wr amperach obwodu nieliniowego

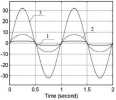
Rys. 8. Przebieg wartości chwilowych symulowanych spadków napięć w obwodzie nieliniowym w woltach: 1) dla rezystancji R/ = in, 2)R₂ = 1/^jQ,3)R,= l^n

Rozważmy szeregowy obwód dla prądu przemiennego (rys. 9).

Na schemacie przyjęto wartości zespolone prądu, napięć i impedancji, określone następująco:

U, = |C/r| e'^,0° = 20 d*°° V,	(3)
Z,=R,+X,= 1 + ijn.	(4)
Z2 = R2+X2 = l + 5j£2.	(5)
Z3 = R3+X3 = 1 -2j£2.	(6)
/ = |/| e"’',	(7)
U, = \U,\ e"'.	(8)
U2=\U2\d’^2,	(9)
	(10)

Dla porównania wyników obwód został rozwiązany metodami tradycyjnymi, wyliczając impedancję zastępczą, zespolony prąd oraz zespolone spadki napięć:

Dla wyszukanych rozwiązali sporządzono wykres wektorowy (iys. 10) zachowując proporcje między wektorami i obliczone przesunięcia fazow e.

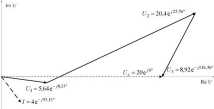
Rys. 10. Wykres wektorowy rozkładu napięć i prądów obwodu z rys. 9

Na podstawie ry sunku 10 możemy zauważyć, że suma składowych wartości rzeczywistych spadków¹ napięć w obwodzie jest równa wartości rzeczywistej napięcia zasilania. Natomiast suma składowych wartości urojonych spadków napięć jest równa zero (równa wartości urojonej napięcia zasilania). W rozważanym przypadku możemy ułożyć następujące zależności:

\Ui\ cos ip, + \U₂\ cos tp₂ + |(/j| cos ę₃ = U_z, (16)

\Ui\ sin ę>, + \Uj\ sin q>₂ + |Oj| sin tp₃ = 0.    (17)

Rozważmy rozwiązanie równań (16 i 17) przez układy automatycznej regulacji, które dobierają wartość prądu i przesunięcia fazowego prądu. Są to dwa układy regulacji stalowartościowej z wewnętrznym powiązaniem dwóch zmiennych I i ę,. Strukturę modelu rozwiązującego omawiane równania w programie Simulink przedstawia rysunek 11.

W chwili czasu 0,5 s załączone zostaje napięcie zasilania. Przebieg ustalony (okno Graph) daje rozwiązanie. Otrzymane przebiegi ilustruje rys. 12.

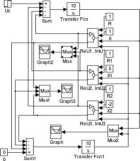
Rys. 11. Stniktura modelu w programie Simulink rozwiązująca równania (16 i 17)

Z, = 3 + 4j = 5 e*^53-1’ £2,

(11)

Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki PG, ISSN 2353-1290, Nr 47/2015

17