1109810760

MODELOWANIE MATEMATYCZNE KINETYKI SUSZENIA... 131

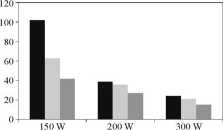
Rys. 1. Czas suszenia liści bazylii w zależności od parametrów procesu Fig. 1. Drying time of basil leaves depending on the parameters of the process

peraturze powietrza 30°C; b_150_40 - bazylia suszona mikro falowo-konw ekcyj-nie przy' mocy mikrofal 150 W i temperaturze powietrza 40°C; b_200_20 - bazylia suszona mikrofalowo-konwekcyjnie przy mocy mikrofal 200 W i temperaturze powietrza 20°C: b_200_30 - bazylia suszona mikrofalowo-konwekcyjnie przy mocy mikrofal 200 W i temperaturze powietrza 30°C: b_200_40 - bazylia suszona mikrofalowo-konwekcyjnie przy mocy mikrofal 200 W i temperaturze powietrza 40°C; b_300_20 - bazy lia suszona mikrofalowo-konwekcyjnie przy⁷ mocy mikrofal 300 W i temperaturze powietrza 20°C; b_300_30 - bazylia suszona mikrofalowo-konwekcyjnie przy mocy mikrofal 300 W i temperaturze powietrza 30°C; b_300_40 - bazylia suszona mikrofalowo-konwekcyjnie przy mocy mikrofal 300 W i temperaturze powietrza 40°C.

Na podstawie analizy współczynników determinacji (R²) można stwierdzić, że większość z zastosow anych modeli matematy cznych dobrze opisywała dane doświadczalne. Wartości R² mieściły się w zakresie od 0,849 do 0,999, pr^ czym najmniejszą wartość zanotowano w przypadku modelu nr 4. który opisywał suszenie przy parametrach 150 W i 40°C. Również małe wartości RMSE oraz X², wahające się odpowiednio w granicach od 0.0053 do 0.1281 oraz od 0.00003 do 0,02051. wskazują na dobre dopasowanie wybranych modeli matematycznych. Współczynnik zmienności resztowej wskazuje, o ile procent średniej arytmetycznej empirycznej względnej zawartości wody (MR) wartości przewidyw ane danym modelem odchylają się od doświadczalnej względnej zawartości wody. Na ogól przyjmuje się, że wartości współczynnika zmienności resztowej, wynoszące do 20%, informują o praktycznej możliwości zastosowania danego modelu matematycznego. W opisywanym eksperymencie V_e przyjmowało wartości od 2 do 42%. Najmniejszymi wartościami współczynnika zmienności resztowej charakteryzował się model nr 5 oraz nr 2. Jednakże ze względu na fakt, że w niektórych przypadkach (b_150_40, b_200_30, b_300_40) na podstawie modelu nr 5 (model Midilliego i in.) przewidywano ujemne wartości względnej zawartości wody (a w przebiegu krzywej suszenia obserwowano ekstremum) za optymalny uznano model Pagea [Sarimeseli 2011],

Warto jednak zauważyć, że w wielu publikacjach naukowych model Midilliego i in. [2002] występuje jako model najlepiej opisujący dane uzyskane doświad-czelnie [Jakubczyk 2009: Amiri Chayjan i in. 2011], Model Wanga i Singha [1978] okazał się najmniej przydatny do opisu otrzymanych danych. W większości przypadków w przewidywanych tym równaniem krzywych obserwow ano minimum (ekstremum), podobnie jak w wymienionych wcześniej przy padkach opisywanych przez model Midilliego i in. [2002],