1257951424

86

Opierając się na powyższym algorytmie przeprowadzono obliczenia prawdopodobieństwa zniszczenia zespołu wirującego złożonego z tarczy wirnikowej o geometrii pokazanej na rys. 5.20a oraz łopatki cylindrycznej o promieniu zewnętrznym 0,40 m. Jako dane zdeterminowane przyjęto:

-    gęstość materiału p = 7800 kg/m³,

-    obroty wirnika n = 6000 obr/min,

-    moduł Younga E = 2,0 10⁵ MPa,

-    obciążenie tarczy wirnikowej wywołane łopatkami P = 57,6 MPa,

-    współczynnik funkcji Nortona dla tarczy B = 3,0 10 ¹³ MPa“ⁿh^_1,

-    współczynnik funkcji Nortona dla łopatki B = 2,6 10"¹³ MPa^h"¹,

-    współczynnik funkcji zniszczenia A = 0,1 10“⁹ MPa^h^-1,

-    współczynnik rozszerzalności liniowej tarczy i łopatki P = 0,00002 1/K,

-    temperaturę łopatki i tarczy T = 500°C.

1.00000

0.10000

0.01000

0.00100

0.00010

0.00001

0.00000

4000    5000    6000    7000    8000

t[h]

cu

■

c

Ń

N

O

CD

O

O

a

o

cu

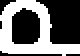
Rys. 6.12. Całkowite prawdopodobieństwo zniszczenia zespołu wirującego Fig. 6.12. Total probability of failure of the rotating unit

Jako wielkości losowe przyjęto:

-    wykładnik funkcji Nortona |Xn = 3, s_n = 0,03,

-    wykładnik funkcji zniszczenia |i_m = 2,5, s_m = 0,025,

-    całkowity luz początkowy p₅ = 0,005 m, Sg = 0,00005 m. Prawdopodobieństwo: zniszczenia łopatki (1), tarczy (2), skasowania luzu

(3) oraz prawdopodobieństwo całkowite zniszczenia zespołu wirującego (4) podano na rys. 6.12. Dla powyższych danych całkowite prawdopodobieństwo zniszczenia zespołu wirującego jest praktycznie równe prawdopodobieństwu skasowania luzu promieniowego. Wpływ prawdopodobieństwa zniszczenia łopatki i tarczy jest pomijalnie mały.