1484605285

18

2.4. Ruchliwość W

Ruchliwość łańcucha (układu kinematycznego) lub stopień ruchliwości (W) w sensie fizycznym oznacza (przy pewnych zastrzeżeniach [11]) liczbę stopni swobody jakimi dysponują człony łańcucha względem jednego z nich, np. podstawy. Na podstawie prostego przykładu łatwo się zgodzić z tym, że w czworoboku ABCD (rys. 17a) człony 2,3 i 4 dysponują względem podstawy 1 tylko jednym stopniem swobody. W tym przypadku można wymusić na członie 2 ruch obrotowy, wtedy już jednak człony 3 i 4 pozostają w ruchu nadążnym - ściśle określonym. Takiemu układowi przypisać należy ruchliwość W - 1.

W kolejnym układzie (rys. 17b) można niezależnie od siebie wymuszać ruchy dwóch członów, np. ruch obrotowy członu 2 i postępowy ruch członu 5 względem podstawy. Temu układowi przypisać należy ruchliwość W = 2.

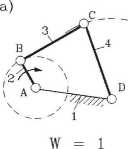
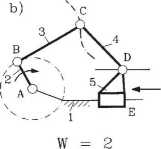
Rys. 17. Przykłady łańcuchów kinematycznych o różnych ruchliwościach

Korzystając z wprowadzonych pojęć ruchliwości można powiedzieć inaczej, że ruch członów układu jest jednoznacznie określony gdy liczba członów czynnych n_c odpowiada ruchliwości W (n_c =W). Oczywiście układy ruchliwe mają W> 1, układy sztywne zaś lub przesztywnione W < 0.

Ruchliwość W w przypadku łańcuchów prostych można bez trudu oceniać intuicyjnie. W wielu jednak układach bardziej złożonych, a zwłaszcza przestrzennych, intuicja zawodzi. Aby się o tym przekonać, wystarczy rozpatrzeć przykładowo prosty układ przestrzenny przedstawiony na rys. 18. Czy jest to układ ruchliwy czy nieruchliwy? Jaką przypisać temu układowi ruchliwość W?

W takich sytuacjach należy korzystać ze znanych wzorów strukturalnych. Przypomnijmy:

(i)

W = 3(n - 1) - 2/7, -p₂ (dla układów płaskich)

W = 6(n - 1) - 5/7, - 4/7₂ — 3/7₃ — 2p₄ - p₅ (dla układów przestrzennych) (2)