1492316942

Algebra Boole’a (3)
4 przemienność
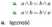
«. («Afc)A<r-«A(*Ac) «. (ffVfr)Vc=<rV(/»Vc)
a «V(frAc)ss(flVi>)A(flVc) a AA(fcVc) = (flAfr)V(flAc)
L
Algebra Boole’a (2)
L
Wyszukiwarka
Podobne podstrony:
3 4 KRATY I ALGEBRY BOOLE ’A Wniosek 4.27. Krata wszystkich podgrup grupy przemiennej jest modularna
Aksjomaty algebry Boole a • prawo przemiennosci Xj+X2 = X2+Xj i,r2=x2x, •
4 4 KRATY I ALGEBRY BO OLE ’A 4.3 Reprezentacje krat rozdzielnych i algebr Boole’a Definicja 4.31.
5 4 KRATY I ALGEBRY BOOLE ’A Twierdzenie 4.36. Każda krata rozdzielna jest izomorficzna z pewną krat
Image048Rozdzial3 Rozdział PODSTAWY TEORII UKŁADÓW CYFROWYCH3.1. Wstęp Algebra Boo
Image051 V Zestawienie zasadniczych twierdzeń algebry Boole’a Tablica 3.1 1 a A
Algebra Boole’a - operacje logiczne operacje tylko na zmiennych dwuwartościowych: -
W4. Algebra Boole a. Funkcje logiczne. Metody reprezentacji funkcji logicznych. W5. Logika i teoria
II UKŁADY PRZEŁĄCZAJĄCE 2.2. Dwu elementowa algebra Boole’a Dwuęlementowa algebra Boole a jest to
Zadanie domowe Wykorzystując aksjomaty i twierdzenia algebry Boole a dowieść następujących
img026 (35) 1/64fvu- ^jamouaa /i-kubi--Mj ~z- prxe.lo yux<M€uA (ac óącfajC- VC J + IM 6k* r
więcej podobnych podstron