1588093940

Elementy macierzy S₀,, (s₀),j przyjmują wartości 1 jeśli obszar identyfikowany wartością i graniczny z obszarem j, (i, j e {7, II, ... , VI}).

i    o

il    1

iii    1

iv    o

v    o

vi    o

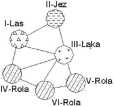
II III IV V VI 110 0 0 0 10 0 0 10 111 0 10 0 1 0 10 0 1 0 1110

Rys.4. Zapis sąsiedztwa obszarów, przedstawionego w formie graficznej G₀ i macierzowej S_G, otrzymany z macierzy Z₀-_K

Krawędzie grafu G₀ opisane są w macierzy Z₀._K, jako linie rozgraniczające obszary. Można je wszystkie wprowadzić do zapisu graficznego G₀, otrzymując kolejny model G₀.k (rys.5).

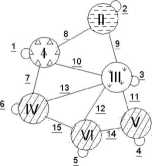
Rys.5. Przedstawienie graficzne sąsiedztwa obszarów z liniami granicznymi rozgraniczającymi te obszary i liniami granicznymi kompleksu obszarów za pomocą grafu G₀-k

Poszukajmy jeszcze relacji między obszarami a węzłami i zapiszmy je w macierzy Z_w.₀. Otrzymać je możemy wykonując działanie:

Zw.o=((Zo.kKZw.k)^T)/2.    (6)

Wyrazy tej macierzy przy jmują wartości równe 0, 1. Wartości macierzy (Zo_W)jj równe 1 wskazują na węzeł identyfikowany wartością j (j=l, 2, ..., 12) jako punkt graniczny obszaru i (i=I, II, ..., VI).

Tablica 4. Macierz zależności Z_n.w miedzy obszarami a węzłami grafu G

5