365605313
n(n\ m) n! m
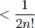
Z takimi n i m tworzymy liczby m
T\ =n\ — 1, T2 = 2n\ — 1, ..., Tm = mn\ — 1
Zauważ ,że żadne z T nie ma czynnika pierwszego < n lub > mn!. Co więcej jeśli p | Ti i p | Tj wtedy p | (Ti - Tj) tak ,że p | (i - j). Innymi słowy, wileokrotności p są p poza naszym zbiorem liczb. Stąd nie więcej niż UL _|_ l liczb podzielnych przez p. Ponieważ każda liczba ma przynajmniej jeden czynnik p ■ pierwszy mamy
lub
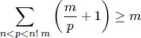
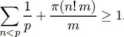
Ale teraz (1) i (2) z prawej strony powinny być <1 i mamy sprzeczność, która dowodzi naszego twierdzenia.
Dowód Eulera który jest bardziej istotny, zależy od jego bardzo ważnej tożsamości
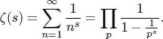
Tożsamość ta jest zasadniczo analitycznym wyrażeniem twierdzenia o jednoznacznym rozkładzie na czynniki. Mamy
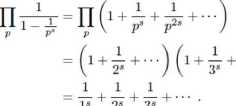
r
2S 3l
)(
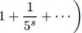
Euler twierdził ,że dla s=l
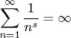
tak więc
Wyszukiwarka
Podobne podstrony:
Krok 2. Kiedy będziemy indukcyjnie tworzyć automaty dla podformuł naszej formuły, zauważymy, że będz
Dla wszystkich całek można zauważyć, że wraz ze wzrostem n (liczby losowanych punktów),
Scan10016 Zauważmy, że i2=(0,lX0,I)*(-l/0)=-l Każda liczba zesDoiona (a,b) da się przedstawić za pom
051 2 Równania i nierówności wymierneSprawdzamy, czy znalezione liczby należą do dziedziny. Zauważ,
10 (64) 215 Formy różniczkowe podczas gdy 2n ydx = — jabs
DSC00181 2 ifipwit tlliłftin wfi ant . W xm t t.tM.Mn o MtN
Ćwiczenie 1. Dynamiczne własności tranzystora IGBT (8.4.2006) 11 Należy jednak zauważyć, że w chwili
wzrost liczby ludności. W metropolii Warszawy i Krakowa zauważalny jest wzrost liczby mieszkańców w
PRZYKŁAD Aby się przekonać, że dla n > 5 mamy n2 < 2n. Zauważamy, że dla n=5 nierówność jest
52472 Untitled Scanned 12 (12) 15 61. W Udowodnić, że jeżeli liczby a. <t2.....a„, gdzie n >
PRZYKŁAD Aby się przekonać, że dla n > 5 mamy n2 < 2n. Zauważamy, że dla n=5 nierówność jest
czasowniki czas, liczby 7 T J* - r T*T2 I . ; ^ : Ihtrr.ir. -T:;- J*: ..‘“rtf---.. ,u. r v/*
PRZYKŁAD Aby się przekonać, że dla n > 5 mamy n2 < 2n. Zauważamy, że dla n=5 nierówność jest
PRZYKŁAD Aby się przekonać, że dla n > 5 mamy n2 < 2n. Zauważamy, że dla n=5 nierówność jest
Przepływy pieniężne netto mogą tworzyć liczby o różnych wartościach i o różnych znakach. Z reguły
PRZYKŁAD Aby się przekonać, że dla n > 5 mamy n2 < 2n. Zauważamy, że dla n=5 nierówność jest
PRZYKŁAD Aby się przekonać, że dla n > 5 mamy n2 < 2n. Zauważamy, że dla n=5 nierówność jest
PRZYKŁAD Aby się przekonać, że dla n > 5 mamy n2 < 2n. Zauważamy, że dla n=5 nierówność jest
więcej podobnych podstron