4307685596

Ek = \^mvl + \^mvl + \^mvl

Zgodnie z zasadą ekwipartycji energii, średnia energia każdego z członów wynosi;

:T, gdzie k jest stałą Boltzmana

stąd średnia energia atomu wynosi \kT, a średnia energia jednego mola atomów wynosi | RT (R - stała gazowa). Całkowita energia wewnętrzna jednego mola gazu doskonałego, wynosi:

U_m = U_m{0) +

gdzie U_m(0) - oznacza molową energię wewnętrzną gdy T = 0, stąd:

(i)_v“^=r⁸-^31[J-^K_1'^morli

= 12.48 [J • K"¹ • mol"¹] = C_v

Gdy gaz składa się z cząsteczek wieloatomowych (ułożonych w sposób nieliniowy) oprócz ruchu translacyjnego w trzech wymiarach, cząsteczki mogą wykonywać rotację wokół trzech osi. Pojawia się (zgodnie z zasadą ekwipartycji energii nowy wkład energii pochodzący od rotacji, Eu = \RT. Dla cząsteczek liniowych \RT. Całkowita energia wewnętrzna (dla cząsteczek nieliniowych) wynosi wtedy:

U_m = U_m(0) + |RT = 2 • 8.31 = 25 J ■ K^_1 • mor¹ stąd pojemność cieplna:

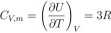
i odpowiednio dla gazu składającego się z wieloatomowych cząsteczek liniowych;

U_m = U_m(0) + ^RT

C_Vm=(~) = -J? =-• 8.31 [J • K-¹ ■ mor¹]

¹ \ar)_v 2    2    ^1    1

Energia wewnętrzna gazu wieloatomowego o nie liniowych cząsteczkach rośnie dwa razy szybciej z temperaturą i pojemność cieplna jest dwa razy wyższa, w porównaniu do gazu jednoatomo-wego. Na wartość energii wewnętrznej, składa się (w przypadku cząsteczek wieloatomowych) również człon pochodzący od energii ruchu oscylacyjnego, jednakże ten rodzaj energii nie można opisać w sposób klasyczny, gdyż energia związana z ruchem oscylacyjnym jest kwantowana. Wyrażenie na średnią energię oscylatora o częstości n ma postać:

8