4831622756

Transmission des ondes de marće k travers l'aquifi>re cótier de Kras 315

R. D e g a 11 i e r -1978-) ainsi que dans les aquiferes karstiąues (L. M o u 1 -lard, B. Mijatović, R. Kareh etB. Masaad -1965-, J. C. Garnie r et C. L. Clarion -1967-, M. Razack, C. Drogue, C. Roma-riz et C. Almeida -1980-).

2.2.2. Nappe semi-captive

Supposons maintenant que l'aquif$re ćtudić (permćabilitć horizontale K, epaisseur M) soit en communication a travers son eponte semi-permeable (per-meabilite verticale K', epaisseur M') avec une nappe a niveau d'eau constant. C’est le schema classique de la drainance.

D’apres E. De Cazenove (1971), la grandeur caract£ristique B (distance de drainance):

B = /M M⁷ K/K'

est liee k un parametre d different de zero, caracterisant 1’intensite de la drainance. par:

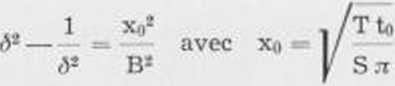
L’ćquation de diffusivitć et sa solution seerivcnt:

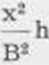
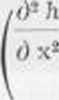
2 óh

dt²*'

\ to

h (x, t)

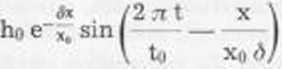
Les valeurs de Tamortissement et du dephasage permettent de deduire xo/<5 dune part, et d’autre part, dou xo, * et B. A partir de ces valeurs la diffusivite D peut etre calculee aisement.

2.2.3. Nappe librę

Dans la mesure ou les variations periodiques du niveau h sont faibles par rapport k 1'ćpaisseur de la zonę saturee de l'aquifere, il est admis d'appliquer les equations valables pour les nappes captives (E. De Cazenove, 1971).

2.2.4. Nappe librę avec un ejjet d’ćgouttement

Dans le cas d'un aquif£re librę, avec un effet d egouttement non nćgligeable, en communication directe avec la mer (la methode d‘interprćtation presentee ci-apres suppose maintenucs toutes les autres hypotheses du §2.1.), l’ćquation de la diffusivite s‘ecrit (par analogie avec le phenomene de drainance):

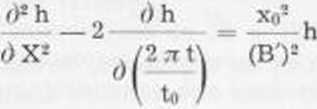
avec