5109637436

Alternatywną metodą do obliczenia objętości wykorzystuje informację o długościach wektorów prostych i kątach pomiędzy nimi.

Niekiedy do odzwierciedlenia struktury geometrycznej sieci Bravais wygodniej jest zamiast komórek prostych posługiwać się większymi komórkami elementarnymi. Komórki proste są więc takim rodzajem komórek elementarnych, których objętość jest najmniejsza z możliwych. Poniższy rysunek pokazuje przykład komórki prostej oraz wygodnej komórki elementarnej w kształcie plastra miodu dla dwuwymiarowej sieci heksagonalnej.

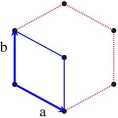
Porównanie komórki prostej (linie ciągle) oraz umownej komórki elementarnej (linie przerywane) dla dwuwymiarowej sieci heksagonalnej, których objętości różnią się trzykrotnie.

2.2 Typy sieci

Dla dwuwymiarowych struktur krystalicznych można wyróżnić kilka rodzajów sieci Bravais, które są ustalone na podstawie niezmienniczości na transformacje obrotu i odbicia zwierciadlanego. Można scharakteryzować je za pomocą długości wektorów prostych oraz kątem (f>:

•    sieć kwadratowa ..........................................................a = b,    <j) = 90°

•    sieć prostokątna ..........................................................a^6,    <p = 90°

•    sieć prostokątna centrowana    wewnętrznie .................................a / 6,    <f> — 90°

•    sieć heksagonalna........................................................a = b, (j>= 120°

•    sieć skośna....................................................(j) ^ 90° i <j) ^ 120°.

3