0402

404

XII. Ciągi i szeregi funkcyjne

2) Zastosujemy analogiczną metodą do obliczenia sumy szeregu dwumiennego

y =/(¹) = 1 +mx^Jr "»>■-!> _X2+ ... ₊ .«(¹-!) ...(«-»+!) _x.₊ ...

1-2 1 • 2¹... •«

(tym razem ustalone jest m, a. x zmienia się w przedziale (—1, 1); porównaj 439, 4)). Różniczkując go wyraz za wyrazem otrzymujemy

f'(x) = ,„[l+(„,-!)¹+ (m^ll(mzJL_x2₊ ... ₊ _(/»—l).(m—2) ... (/»—»)    1

l    1-2    1-2- ... -n    J

Teraz już łatwo zauważyć, że

(1 +¹)/'(¹) = łi>/W(‘).

A więc nasza funkcja spełnia równanie różniczkowe

(l+¹)y = my,

skąd

y = <7(1+¹)".

Ponieważ dla x = 0 jest oczywiście y = 1, więc stała C = li ostatecznie

y=f{x) = (1+¹)"¹ •

3) Wiemy już, że suma szeregu Dirichleta [385, 3)]

00

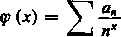
n- 1

jest dla x> A (gdzie 2 jest graniczną odciętą zbieżności, A< + oo) funkcją ciągłą [439, 2)]. Różniczkując wyraz za wyrazem możemy otrzymać pochodną tej funkcji

<p'(x) = — 2^‘In n (x > X) .

1

Wynik ten otrzymaliśmy na razie tylko w sposób formalny. Żeby go uzasadnić, wystarczy sprawdzić że ostatni szereg jest zbieżny jednostajnie względem x dla wszystkich x > x₀, gdzie x₀ jest dowolną, lecz ustaloną liczbą większą niż A. Tak samo jak w ustępie 439, 2, otrzymujemy to na podstawie kryterium

ln n

Abela, korzystając z tego, że czynniki —_■■■■■ poczynając od n = 2 maleją wraz ze wzrostem n i są

n o

wspólnie ograniczone liczbą ln 2. Dowolną wartość x>}. możemy zawrzeć między pewnymi liczbami x'>X i x">x'. W przedziale <¹', ¹"> stosuje się już twierdzenie 7 [435].

W ten sam sposób można przekonać się o istnieniu pochodnych wszystkich rzędów funkcji <p (x), które można przedstawić w postaci szeregów.

m (iw—1) ... (im—n+1) 1 ... •«

1

Przy mnożeniu f’{x) przez 1 +x trzeba skorzystać z następującej własności współczynników dwumianu:

(m— 1) (m—2) ... (iw—n) , (»i— 1) (m—2) ... (m—n+1) 1-2- ... -n    1-2- ... (n-1)

której szczególnym przypadkiem jest znana zależność