0434

436

XII. Ciągi i szeregi funkcyjne

425. Szereg Lagrange’a. Zastosujmy twierdzenie z ustępu 450 do równania szczególnego postaci (25)    y = a+xtp{y),

gdzie o funkcji q> (y) zakładamy, że jest analityczna w punkcie y = a. Wtedy, jak już wiemy, dla dostatecznie małych wartości x można stąd wyznaczyć y jako funkcję zmiennej x, analityczną w punkcie x = 0 i przyjmującą w tym punkcie wartość a.

Niech u — f(y) będzie jakąś funkcją zmiennej y, analityczną dla y = a. Gdy zastąpimy tu y przez wspomnianą funkcję zmiennej x, to u będzie funkcją zmiennej x też analityczną w punkcie x = 0. Postawmy sobie za cel rozwinąć u według potęg x, dokładniej: otrzymać wygodne wzory na współczynniki tego rozwinięcia.

Zauważmy uprzednio, że gdy zmienną jest a, wówczas y można wyznaczyć z równania (25) jako funkcję dwóch zmiennych x i a analityczną w punkcie (0, a) ('). Zmienna u będzie wtedy także funkcją tych samych dwóch zmiennych.

Różniczkując (25) względem x i względem a otrzymujemy

[\~xą>'[)O)-^ = <p(y),    [1—= 1,

Sx    da

ox    da

8x    da

skąd oczywiście (26)

i ogólnie dla u = f(y) (26a)

Z drugiej strony, dla dowolnej funkcji F(y), dla której istnieje pochodna względem y, mamy

(27)

_0_

dx

Kt

]

&_

^rća

[

Łatwo można się o tym przekonać bezpośrednim różniczkowaniem i powołaniem się na tożsamości (26) i (26a).

Ze wszystkich tych uwag skorzystamy przy dowodzie bardzo potrzebnego nam dalej wzoru

(28)

S"u

0*"

a»-i

0a"-^ł

[

<p’(y)

6u_ 1(^J)

da J

Dla n = 1 sprowadza się on do (26a). Założymy teraz, że jest on prawdziwy dla pewnej wartości n > 1 i udowodnimy, że jest wówczas prawdziwy dla pochodnej rzędu n +1. Różniczkując (28) względem x i korzystając z prawa [190] zmiany kolejności różniczkowania otrzymujemy

dⁿ⁺¹u

0x"⁺¹

0—¹

go"-¹

_g_

dx

I f"(y) •

du_

da

]

Ale na mocy (27) i (26a) otrzymujemy kolejno

8u_ 1

gflj

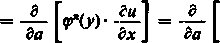
<p*⁺‘(y)-

du 1

go J '

(‘) W twierdzeniu tym zakłada się, że twierdzenie ustępu 450 obejmuje przypadek, gdy w równaniu występują trzy zmienne i jedną z nich wyznaczamy jako funkcję dwu pozostałych.

(²) <p"(y) oznacza tu potęgę [<p (y)]\