0386

388

XII. Ciągi i szeregi funkcyjne

regiem potęgowym (31) w przedziale jego zbieżności, będziemy mieli wszędzie wewnątrz tego przedziału

/(x) =    x+a₂ x²+a₃ x³ + ... +a_H x"+ ...

/'(*) = 1 -fli+2 -a₂ x + 3 -a₃ x² + ... +n-a,,x"-¹+ ...

/"(*) = 1-2 -a₂+2 -3 •a₃ x+ ... +(n-l) •n •a_n x*^_J+ ...

/'"(*) = 1-2-3-0,+ ... +(n—2) (n —1) n a_H x"^_3 + ...

f<”\x) m 1 -2-3- ... •(n — 1) •na„+ ...

Jeżeli we wszystkich tych równościach przyjmiemy x = 0, to otrzymamy dobrze znane wyrażenia na współczynniki szeregu potęgowego

«o =/(0),

/^(O)

2!

/'"(O)

3!

[porównaj 403, (7)]. Gdybyśmy rozpatrywali szereg w ogólnej postaci (31*), to zamiast wartości x = 0 podstawilibyśmy po prostu x = x₀. A więc:

9° Funkcja przedstawiona przez szereg potęgowy w przedziale jego zbieżności ma wewnątrz tego przedziału pochodne wszystkich rzędów. Sam szereg w stosunku do tej funkcji jest niczym innym, jak jej szeregiem Taylora.

To ciekawe twierdzenie wyjaśnia zagadnienie rozwinięcia funkcji w szereg potęgowy, którym zajmowaliśmy się w poprzednim rozdziale. Widzimy, że jeżeli funkcja w ogóle da się rozwinąć w szereg potęgowy, to właśnie w szereg Tyalora. Dlatego też ograniczyliśmy się właśnie do badania, czy funkcja jest równa sumie swojego szeregu Taylora. Zauważmy przy tym, że funkcja, która daje się rozwinąć w szereg Taylora według potęg x—x₀ nazywa się analityczną w punkcie x₀

Wyłożoną teorię stosuje się także do wielokrotnych szeregów potęgowych. Zatrzymamy się na szeregu o dwóch zmiennych

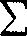
fln(x-x₀)'(>’->’o)'^t •

l,k-0

Wewnątrz obszaru zbieżności [396] szereg ten można różniczkować wyraz za wyrazem dowolną liczbę razy. Stąd, tak jak poprzednio, łatwo można otrzymać wzory na współczynniki :

tfoo — /(*Ol M

^ai o —

Sf(x₀, y₀) dx

^a0l —

d/(x₀, y₀)

dy

S²f(xo, yo) dx²

i ogólnie

₌ _L d‘^+l7(xo, y₀) “ i!Ar! ‘ dx‘8y^k'