0388

390

XII. Ciągi i szeregi funkcyjne

gdzie {o„} jest pewnym ciągiem liczb rzeczywistych. Przypuśćmy, że nie jest on „wszędzie rozbieżny”, więc ma on skrajną!¹) odciętą zbieżności A< + oo. Dla dowolnej liczby x₀>A szereg

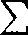
a.

n^xo

jest zbieżny. Stąd wynika już, że rozpatrywany szereg jest zbieżny jednostajnie dla wszystkich x>x₀ [twierdzenie analogiczne do 1 z ustępu 437], Twierdzenie to wynika z kryterium Abela, jeżeli napiszemy nasz szereg w postaci

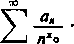
1

rt^x~*o

i zauważymy, że czynniki l/n'-'⁰: maleją wraz ze wzrostem n i są przy tym wspólnie ograniczone przez 1. Wtedy z twierdzenia 1 wynika, że suma szeregu jest ciągła dla x->at₀, a więc (z uwagi na dowolność x₀) dla wszystkich x>X [twierdzenie analogiczne do 2°].

Jeśli A jest skończone i szereg

a.

n¹

jest zbieżny, to w ten sposób stwierdzamy zbieżność jednostajną rozpatrywanego szeregu dla x>X [porównaj 5°] i ciągłość prawostronną jego sumy dla x = A [porównaj 6°].

3) W ustępie 390, 6) po określeniu funkcji E (x) za pomocą równości

OO

n;

*— i

stwierdziliśmy, że spełnia ona taką zależność:

(I)    E{x+y) = E(x)-E(y).

A więc, zgodnie z twierdzeniem 2° z 437 funkcja E (jc) jest ciągła w danym przedziale od — oo do + oo. A na podstawie wyników 75,1° rozwiązanie ciągłe równania (1) musi mieć postać E(x) = a*. Wreszcie podstawę a wyznaczamy oczywiście z równości

00

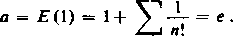
■ -I

A więc ostatecznie E(x) = e* [porównaj 404, (11)].

4) Podamy teraz nowe podejście do szeregu dwumiennego [407, (22)].

1 +mx+

m(m— 1) _x2 . 1-2

m (m—1) (m —2)    ₃ ,

1-2-3

, m (w— 1) , 1-2

I2=5±!!*■+ ....

..•n

który jest zbieżny bezwzględnie dla dowolnego m, gdy |x| < 1. Postawimy sobie za zadanie obliczyć jego sumę. Oznaczmy tę sumę, jako funkcję m (przy ustalonym x, |jc| < 1), przez <p (m).

Z algebry wiadomo, że dla m naturalnego (szereg urywa się wtedy na (m-f l)-szym wyrazie) <p (m) = = (1+j:)". Udowodnimy, że równość ta zachodzi dla każdego m.

Obierając dowolne k, rozpatrzmy podobny szereg

1 +kx+

k(k-1)    , A (A —1) (Ac —2)    ₃    . k(k-l) ...(k-n+l) ^ .

1-2    1-2-3    1 -2-... i»

(') Chodzi tu o taką liczbę A, że dla x₀< A szereg jest rozbieżny (przypisek redakcji wydania polskie

go).