0416

418

XII. Ciągi i szeregi funkcyjne

jest zbieżny, o czym łatwo możemy się przekonać stosując kryterium d'Alemberta, więc w poprzednim szeregu możemy zgodnie z twierdzeniem połączyć wyrazy podobne

(1+*)"- ...) + ...

Z drugiej strony, oczywiście

(H-x)“ —    "+*> — 1+a In (l + x)4- ...

Ponieważ oba rozwinięcia muszą być identyczne, więc porównując współczynniki przy a otrzymujemy

łn(i+z-) = x-4r + ^Jr-- -

2    3

Zauważmy teraz, że udowodnione twierdzenie możemy stosować także do szeregów wielokrotnych na przykład do szeregu

2 ^a,km *"} ■

n-0

Rzeczywiście, wystarczy tylko zastąpić szereg podwójny przez zwykły, żeby sprowadzić zadanie do przypadku już rozpatrzonego.

446. Superpozycja szeregów. Rozpatrzmy funkcję y =/ (x), którą można rozwinąć w szereg potęgowy (I) w przedziale (—R, R). Niech oprócz tego, dana będzie funkcja <p(y) także rozwijalna w szereg potęgowy

(6)

<p(y) = V ^h,n y

in=0

ho + hi y+h₂y²+ ... +h_my^m+ ...

dla wartości z przedziału (— p, p).

Jeżeli |a₀l = 1/(0)! <p, to dla dostatecznie małego x mamy |/(x)| < p, a więc ma sens funkcja złożona <p (/(x)).

Jeżeli tylko |cr₀| < P. to funkcję <p (f(x)) można w otoczeniu punktu x = 0 rozwinąć w szereg względem potęg x w ten sposób, że podstawiamy do (6) za y szereg (1), dokonujemy wszystkich operacji podnoszenia do potęgi zgodnie z (4), a następnie łączymy wyrazy podobne. Dowód. Przyjmując, że |x| < R rozpatrzmy szereg

00

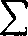
= k>l + |fllN*l + |tf2|-M²+    + \°n\ ' M"+    ■

wobec ciągłości jego sumy [437, 2°] i z uwagi na to, że |o₀! < P, dla dostatecznie małych x spełniona jest nierówność

(7)    \a« x”\ <p,

7^0

a zatem szereg

l*ol+f>J (£ M-\x\ⁿ)^m

m=l    ««0

jest zbieżny.