0444

446
DII. Ciągi i szeregi funkcyjne
jest bezwzględnie zbieżny dla dowolnej zespolonej wartości z, podczas gdy szeregi
o
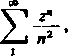
GD
1
z*
n
mają promień zbieżności R — 1.
Na brzegu koła zbieżności szeregi mogą się zachowywać różnie. Tak spośród trzech przytoczonych przed chwilą szeregów pierwszy jest wszędzie rozbieżny na okręgu |z| = 1, ponieważ nie jest spełniony zasadniczy warunek konieczny zbieżności: wyraz ogólny nie dąży do zera. Drugi szereg jest zbieżny bez-
względnie we wszystkich punktach tego okręgu, bo szereg —j- jest zbieżny. Wreszcie jeżeli w trzecim
1 n
szeregu podstawimy z = cos 0 W sin 0, to przyjmie on postać
V"1 cos nO sin nO
Zj n Z-j n
i (poza przypadkiem 0 — O, tzn. z — I) jest zbieżny [38S, 2)], ale nie bezwzględnie.
Uwaga. Gdy współczynnikami szeregu potęgowego są liczby rzeczywiste (tak jak w poprzednich przykładach), to oczywiście promień R „koła zbieżności” pokrywa się na płaszczyźnie zespolonej z poprzednim promieniem „przedziału zbieżności” na osi rzeczywistej.
Wymienimy teraz inne twierdzenia o szeregach potęgowych, które można przenieść do teorii szeregów potęgowych zespolonych.
Twierdzenia 1 ° i 2° z ustępu 437 zachowują się bez żadnych zmian, a więc wewnątrz koła zbieżności suma (I) szeregu potęgowego jest funkcją ciągłą zmiennej z.
Natomiast twierdzenie Abela [437, 6°] wysłowimy w sposób następujący:
Jeżeli szereg (I) jest zbieżny w pewnym punkcie z0 okręgu |z| = R, to Qdy punkt z dąży do punktu z0 od wewnątrz kola wzdłuż promienia, to
lim £ c„z* = c„rS (').
W szczególnym przypadku, gdy z0 — R, możemy przyjąć, że z = r jest zmienną rzeczywistą dodatnią i równość powyższa przybiera postać:
lim c, r" = ][] c„ R".
'-U-ll ,_o n—o
Gdy podstawimy c. =■ a, | b,i, to rozpada się ona na dwie równości
<n 00 CO CO
lim £ a«r" = 2 a’ R" ‘ lim 2 bmr* = ]>] b„ RT .
r_*R_0 W"0 n-0 B_0 n-0
Ponieważ szeregi po prawych stronach są zbieżne z uwagi na zbieżność szeregu
J c. ** = J (fl.+ó. i) RT,
n«0 n-0
więc do dowodu tych równości wystarczy powołać się na zwykłe twierdzenie Abela.
Przejdźmy do przypadku ogólnego. Przez 0o oznaczymy argument liczby z0. Można wtedy nrzyjąć
z0 = R (cos 60+i sin 0O), z = r (cos 0o+i sin 0O)
(') Można udowodnić, że ta równość zachodzi nawet wtedy, gdy z dąży do z0 w sposób ogólniejszy, jednak nie będziemy się na tym zatrzymywali.
Wyszukiwarka
Podobne podstrony:
416 DII. Ciągi i szeregi funkcyjne Przypuśćmy, że szereg (2) jest identyczny z (1). Otrzymamy wtedy
418 XII. Ciągi i szeregi funkcyjne jest zbieżny, o czym łatwo możemy się przekonać stosując kryteriu
450 DII. Ciągi i szeregi funkcyjne Dochodzimy do wniosku, że logarytm w (dla wjt0) zawsze istnieje i
374 XII. Ciągi i szeregi funkcyjne 432. Uwaga o zbieżności ąuasi-jednostajnej. Jeżeli szereg funkcyj
8 (8) 134 7. Ciągi i szeregi funkcyjne Jest widoczne, że każda funkcja wchodząca w skład rodziny jed
384 XII. Ciągi i szeregi funkcyjne Chociaż liczbę r można wziąć dowolnie bliską R, z poprzedniego do
400 (5) XII. Ciągi i szeregi funkcyjne 10) Rozpatrzmy rozwinięcie (dla
430 XII. Ciągi i szeregi funkcyjne Korzystąjąc z rozwinięcia (12) dla dostatecznie małych / mamy ^(—
MATEMATYKA165 320 VI. Ciągi i szeregi funkcyjne 5. Znaleźć przedziały, w których zbieżny jest
406 XII. Ciągi i szeregi funkcyjne To, że otrzymany szereg jest rzeczywiście wszędzie zbieżny, spraw
420 XII. Ciągi i szeregi funkcyjne szereg ten jest zbieżny dla — 1 <x<. Równość CO £ (2x-x*)m
8 (2) 2 128 7. Ciągi i szeregi funkcyjne że zbieżność nie jest tutaj jednostajna wystarczy zastosowa
8 (4) 130 7. Ciągi i szeregi funkcyjne i szereg ten jest zbieżny jednostajnie na (a, by, to ifda = J
V. Ciągi i szeregi funkcyjne 1. Badanie zbieżności jednostajnej
więcej podobnych podstron