0404

406

XII. Ciągi i szeregi funkcyjne

To, że otrzymany szereg jest rzeczywiście wszędzie zbieżny, sprawdzamy bezpośrednio. Z samego sposobu jego wyznaczania wynika, że przedstawiona przezeń funkcja spełnia równanie.

Zwracamy uwagę czytelnikowi na swoiste wykorzystanie metody współczynników nieoznaczonych. Mieliśmy tu już nieskończony zbiór tych współczynników i musieliśmy skorzystać z twierdzenia o równości szeregów potęgowych zamiast stosowanego zwykle twierdzenia o równości wielomianów.

6) Gauss wprowadził funkcję

l+Y x-

ć—i nl y (y+1) ... (y+i»— 1)

ftel

[szereg hipergeometryczny; patrz 372; 378, 4)]. Różniczkując dwukrotnie ten szereg wyraz za wyrazem (przyjmując |jr| < 1) stwierdzamy, że funkcja ta spełnia tak zwane hipergeometryczne równanie różniczkowe

x (x-l) u’-ly-(/K+fl+l) x] u'+a/?u — 0 .

Pozostawiamy czytelnikowi łatwe, lecz nieco przydługie rachunki. Tu też można zmienić sformułowanie zadania podobnie jak w przykładzie 3).

7) Niech funkcja f{x) będzie określona dla 0 < x < 1 wzorem

u* 1

Wykażemy, że dla 0< jr< I funkcja ta spełnia ciekawe równanie funkcyjne /(■*■)+/( 1—Jr)+ln je• In(1 —jr) — C= const.

Wystarczy w tym celu wykazać, że pochodna względem x wyrażenia po lewej stronie jest tożsamo-ściowo równa zeru:

/'(*)—/'( 1-jt)+ — ln (ł -x)--— In * = 0 .

x l—x

Różniczkując szereg określający funkcję/(x) wyraz za wyrazem otrzymujemy

f'(x) = —Lin (1 —jej;

L-j n x

nail

zastępując x przez 1— x, otrzymujemy

/'(lIn*.

1 —x

Na tym kończymy dowód.

Samą stałą łatwo można wyznaczyć przyjmując, że w udowodnionej zależności x dąży do 1. Z twierdzenia Abela wynika, że granica lewej strony równości

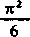
lim /(*) — /(l) *= y ——-x— t—o 4_I n²

g- 1

[440, (4)], a więc C »■ ir^J/6.

8) W 400,4) rozpatrywaliśmy iloczyn nieskończony

J7-£~“

nu 1

Przyjmując, że 0<<p<nl2 logarytmujemy najpierw tę równość [401,4°]: