0466

468

XII. Ciągi i szeregi funkcyjne

Otrzymujemy układ m równości:

Jt0+*
i f At)dt =f(x0)+~-fXx0n £.f"(xo)+ .	. +	W+Po,	1
hJ 2! 3! *0		/«!
Af(x0) - hf\x„)+ ^l/"(jr0)+ .	. +	--‘,-/^,*-^l>(xo)+P,,	/t,
		(m—1)!
W'(a-o) = h*f"(x0)+ •	. +		■^2
		(711-2)!
i^m-^2Af^m~^2(x o) =		—^-/^,"-^,,(jr„)+pM-1	^m-1

Wyrugujmy z tego układu wszystkie pochodne po prawych stronach. Dodamy w tym celu wyraz za wyrazem pierwszą równość do wszystkich pozostałych pomnożonych odpowiednio przez liczby A,, A₂, ... ..., A_m-j, które obieramy w ten sposób, żeby było

(17) +^Ai =0,

— + — Ai+A₂ = 0,

3!    2!

1

+

I

m! (/u— I)!

A,+

(m-2)!

A₂ + ... +A_m~, — 0 .

W wyniku otrzymujemy *0+A

(18) f(Xo) = i- J /(r) dr-Mi żl/(jr₀)+/l_J /izł/'(.r₀)+ ... -M.-. *--*/!/«—«(x₀)+r , *0

gdzie

r

—Po~Ai Pi—A₂ pi— ... —A_m-i p„-3 =

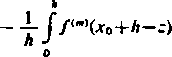
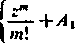
hz^m~' _+A h¹z^m~² (m—1)!    ² (ni—2)!

■*}

lub krócej

li

(18*)    r = - I. [/<">(.*„+h-z) <p_m(z) dz,

0

7"

-^Lr^+/4

m

gdzie przyjęliśmy

(15)    <P»,U)

Ar¹"^-1    , . A^Łz"~^ł ,

(tu—1)! ^{+ 2} (ir»—2)! ⁺ '

Oczywiście z układu równań (17) możemy w sposób jednoznaczny obliczyć kolejno współczynniki /łi, A 2, ..., i to niezależnie od wyboru funkcji fi liczb x₀ i h. Nawiasem mówiąc, współczynniki

te są już nam znane — są to współczynniki    rozwinięcia funkcji    według potęg x [449, (12)]. Rze

czywiście, gdy przypomnimy sobie postać symbolicznych równań

(/S+1)*-)J‘=.0,

o

którym czynią zadość liczby /?, to łatwo się przekonamy, że właśnie liczby są rozwiązaniami równań