0406

408

XII. Ciągi i szeregi funkcyjne

A gdy skorzystamy ze wzoru

t 1

sin x

otrzymamy również rozkład l/sin.v:

—i—=-+y(-D’(—¹—+-7—) =•—+v(—i>" ₂^2x3 2 ■

sin ,v x    \x-tm    x +/nr/    x ^—1    xⁱ—irn*

«»1    n->i

Różniczkując wyraz za wyrazem rozwinięcie ctg x (niech czytelnik sam się przekona, że jest to uzasadnione) otrzymamy jeszcze jedno pożyteczne, rozwinięcie:

—L_=_L+yf_!_+ —!-].

sin²* x² C—i [ (*—im)² {x+inz)² J

10)    Gdy wyjdziemy z rozkładu sinh x na iloczyn nieskończony [408] możemy w podobny sposób dojść do rozwinięć

CC    CO

ctgh -v=-L+ y -jffi ₂ ,    - = —+ V (-!)"—■77 ₂ i‘P-

x    L.1 jr+irir* sinh.v x ^-j    jr-rii w

«>(    ii-i

11)    W 402 wyprowadziliśmy wzór Weierstrassa dla funkcji r(x) [porównaj (16)]:

. p-Xt*

—J—=_t.c, n(_i+jL)

/’(*+!)    I i \ n)

Uwzględniając, że /' (.v+1) = xF (x) i przechodząc do logarytmów, łatwo otrzymujemy (dla x różnego od 0 i ujemnych liczb całkowitych)

ln |r(.v)|--łn |.v| —Cv+

n* ł

Różniczkując ten szereg wyraz za wyrazem otrzymujemy w sposób formalny równość

../» - -±-c+Y(±--LJ\,

P(x)    x    Z_i \n x+nj

«»1

Udowodnimy teraz, że szereg po prawej stronie równości jest zbieżny jednostajnie w dowolnym przedziale skończonym (nie zawierającym ujemnych liczb całkowitych). Rzeczywiście, ponieważ przy tym Ul jest ograniczone: |.r| <M to co najmniej dla //>M będziemy mieli:

J___1_| ₌ Ul    < M

11    jc+/z |    n(n+x) n(n—M)

EM

ii («—Aż) J^est zbieżny, więc z kryterium Weierstrassa wynika zbieżność jednostajna.

Możemy więc powołać się na twierdzenie 7 z 435, a przez to udowodnić samo istnienie pochodnej ln |/⁷(a)| a więc i samej I⁷ (x) itd.

Dodając do prawej strony otrzymanego wzoru szereg

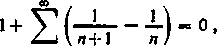
fl- 1