0376

378

XII. Ciągi i szeregi funkcyjne

Tutaj

J

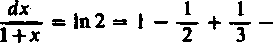
o

więc szereg można całkować wyraz za wyrazem, mimo że dla x = 1 jest on nawet rozbieżny.

Teraz podamy uogólnienie twierdzenia 5 połączone z odrzuceniem żądania ciągłości rozpatrywanych funkcji.

Twierdzenie 6. Jeżeli funkcje u„(x) (n = 1,2, 3, ...) są całkowalne (^ł) w przedziale OC = <a, by i utworzony z nich szereg (3) jest jednostajnie zbieżny, to suma f (jt) szeregu jest też całkowalna i zachodzi (21).

Dowód. Zatrzymamy się na całkowalności funkcji/(*).

Ze zbieżności jednostajnej szeregu wynika, że dla dowolnego e można znaleźć tak duże n, że dla wszystkich punktów przedziału <a, by zachodzi nierówność

(23)

lf(x)-f„(x)l < y e lub f„(x) - Y e < f(x) < f„(x) + y £ .

Weźmy jakąś część <a, /?> przedziału <a, by i niech m, M będą kresami dolnym i górnym funkcji /„(*) w <a, /ł>, a co = M-m jej oscylacją; odpowiednią oscylację funkcji f{x) oznaczymy przez Q. Z uwagi na (23) w przedziale <a, /?> jest

m— yfi <f(x) < M + y c , więc £1 < co-f-e.

Przedział <a, by rozbijemy teraz, jak zwykle, na przedziały częściowe (x_iy x_i+1> i wskaźnikiem i oznaczymy oscylację w /-tym przedziale. Wówczas Q_t < co, +e, więc

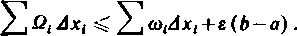
Ponieważ drugi składnik po prawej stronie jest dowolnie mały, a pierwszy dąży do zera wraz z l = max Ax_t, więc to samo jest słuszne i dla lewej strony nierówności, skąd otrzymujemy całkowalność funkcji /(jc) [297, (8)].

Równości (21) dowodzimy zupełnie tak samo, jak poprzednio.

Pokażemy na przykładzie, że bez założenia jednostajnej zbieżności szereg utworzony z funkcji całkowalnych może mieć sumę niecałkowalną. Niech i#„(jr) (dla n — 1,2, 3,...) będzie równe 1 dla .r-ów będących ułamkami nieskracalnymi m/« i równe 0 w pozostałych punktach przedziału <0, ł >. Funkcje te. mające skończoną liczbę punktów nieciągłości, są zatem całkowalne w <0, 1 >, a sumą szeregu jest na pewno niecałkowalna funkcja Dirichleta [300, 2)].

Mimo to zbieżność jednostajna nie jest oczywiście warunkiem koniecznym całkowalności sumy szeregu utworzonego z funkcji całkowalnych. I w tym przypadku Arzela podał warunek konieczny i wystarczający [„uogólniona quasi-jednostajna zbieżność” porównaj 432].

435. Różniczkowanie szeregów wyraz za wyrazem. Korzystając z twierdzenia 5 poprzedniego ustępu łatwo udowodnić

(') W sensie ustępu 295.