0470

472

XII. Ciągi i szeregi funkcyjne

i ogólnie

(2k)l (l+z)« *

a więc warunki nasze są spełnione. Wykorzystąjmy zmodyfikowany wzór Eulera-Maclaurina obcinając go tym razem na wyrazie zawierającym

x

/

_*_ = JL + J- +_L +J_ + _L + _L ₊JL + .L ++

1+z    10    11    12    13    14    15    16    17    18    19

--I-(l-l)--l-fl-J-W

20 \    2/    1200 V 4/

Znajdujemy następnie sumy:

12

7200000

3024000000

(-*)

(0<fl< 1).

— + — + — +. 10 11 12	II +	0,718771403
- —1 20 \	:-D-	-0,025
1 |	'i M-	-0,000625
1200 1	\ 4/
^6 7200000 \	1-—) = 16/	0,000000781

0,693147184

e--—-(i—<0,000000004.

3024000000 V 164/

A więc otrzymujemy z dokładnością do

/

dx

l+x

= ln 2 = 0,69314718 .

3) Pokażemy wreszcie, jak można wykorzystać wzór Eulera-Maclaurina do przybliżonego obliczenia sumy szeregu nieskończonego, co prawda zbieżnego, lecz wolno. Jako przykład weźmiemy szereg

n²

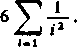
Przyjmijmy w ogólnym wzorze (21) [i (21*)]

f(x) = -i-, h= 1, ó = a+«A, x^{1 2}

gdzie a i n są na razie dowolnymi liczbami naturalnymi. Całkę i pochodne obliczamy łatwo. Podstawiając

1

2

210⁸ -