0446

448

XII. Ciągi i szeregi funkcyjne

457. Funkcja wykładnicza. Widzieliśmy [404, (11)], że dla dowolnego x rzeczywistego mamy

e* = 1+-

1!

X*    xⁿ

■4r+ - +^r +

2!    //!

Jeśli w szeregu tym zastąpimy zmienną rzeczywistą x przez zmienną zespoloną z — x{-yi, to otrzymamy

⁰⁰ H

szereg I +    ° którym wiemy już [456], że jest on zbieżny, tzn. ma określoną skończoną sumę

w całej płaszczyźnie zespolonej. Sumę tego szeregu przyjmujemy właśnie z definicji jako wartość funkcji wykładniczej e* dla dowolnego z zespolonego, tzn. przyjmujemy

O)    ‘‘ = 1+ fi+-F+-+-£+-■

Jak widzieliśmy, definicja ta nie jest sprzeczna ze zwykłą definicją w przypadku wykładnika rzeczywistego, i jest jego naturalnym uogólnieniem.

Gdy skorzystamy z reguły mnożenia szeregów potęgowych, to jak i w 390, 6), przekonamy się łatwo że dla dowolnych wartości zespolonych z i z' będzie

(4)    &-er — e*⁺* ,

a więc charakterystyczna własność funkcji wykładniczej ma miejsce także w zakresie zespolonym.

Funkcja e* jest ciągła na całej płaszczyźnie, a nawet więcej, ma ona wszystkie pochodne ciągłe. Różniczkując wyraz za wyrazem określający ją szereg, otrzymamy, jak poprzednio,

{e‘Y = e*.

Niech będzie z*=x+yi, gdzie x iy są liczbami rzeczywistymi. Zastępując w (4) z przez x, a z' przez yi, otrzymujemy

£»* —

Zajmiemy się teraz specjalnie potęgą e^rl o wykładniku urojonym. Gdy w podstawowej definicji (3) podstawimy yi zamiast z, otrzymujemy

e^rl

H-yi-

2!

iLi- iL

3!    4!

_v2n    _v2n i-1

-2--k_|)» -Ł-/+ ...

(2/ł)!^-    (2n+1)!

lub po oddzieleniu części rzeczywistej od urojonej:

_en ₌

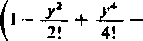
y²‘ (2 »)!

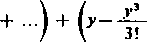
y2»+ I

(2n+l)!

Poznajemy w tych szeregach rozwinięcia cos y i sin >• [404, (12) i (13)] i otrzymujemy stąd ciekawy wzór

(5)    e^r‘ — cos y + i sin y,

który był po raz pierwszy wyprowadzony przez Eulera.

Stąd mamy, na przykład,

_emiU _ j _elt< _ _ |    _e{3Tt!2)l ^ _j    _e2KI _ |

Jeżeli więc z =« x+yi, to

(6)

e' = r^cos y+i sin y) (■) .

(') Moża by przyjąć tę równość jako definicję funkcji wykładniczej o argumencie zespolonym; wzór (4) byłby wtedy wnioskiem z twierdzeń o sumie kosinusa i sinusa.