0420

422
XII. Ciągi i szeregi funkcyjne
a szukamy rozwinięcia funkcji
/(*) =• In g (*) = <ii x+a2 x*+a3 x*+ ... +n« x*+ ...
Łatwo zrozumieć, że współczynniki a i 6 są związane tymi samymi zależnościami (8). Tym razem trzeba wyznaczyć współczynniki a.
5) Udowodnić, że iloczyn nieskończony
FM = f[ (1 +«-*) = (1 +**) (1 +q* x) (1 +q* x) ... (|«| < 1)
M-l
można dla dostatecznie małych x rozwinąć w szereg według potęg x. Wyznaczyć współczynniki tego rozwinięcia.
Dla |jc| < 1 iloczyn jest zbieżny i ma wartość dodatnią: logarytmując go otrzymujemy In F(x) = ln<l+$".*) = (q"x- jq*mx*+ ...) .
n>l m-l
W szczególności szereg ten będzie zbieżny, gdy wszystkie jego wyrazy w nawiasach zastąpimy ich wartościami bezwzględnymi. Stąd [445] wynika, że w otoczeniu zera ln F(x), a wraz z nim [tym razem na mocy twierdzenia z 446] także wyrażenie
F(x) = e‘mr(I},
można rozwinąć w szereg według potęg x.
Dla dostatecznie małych x mamy więc
F{x) = 1+6, x+b2 x*+ ... +b.xm + ....
gdzie należy jeszcze wyznaczyć współczynniki 6,, b2, ..., 6„, ... Najprościej można to zrobić biorąc za punkt wyjścia oczywistą równość:
F(x) = (.\+qx)F{qx),
którą, korzystając z rozwinięcia, można przedstawić w postaci
1+6, x+b2 x*+ ... +6«*"+ ... = (l+<?Jt) (l+biqx+b2q*x2+ ... +b.q*x*+ ...). Stąd na mocy twierdzenia o równości szeregów potęgowych otrzymujemy
biq+q = bt, b2q*+byq2 = b2, .... 6„$*+6.-, q' = 6., ...,
czyli
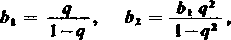
ó.=
i ostatecznie
by
\-q
b2 =
(l-q)(l-qz)
6) Weźmy rozkład funkcji
sin x
na iloczyn nieskończony [408] i jej rozwinięcie w szereg potęgowy
[404, (12)] i porównajmy ich logarytmy [401, 4*]:
czyli
oo .
n
•-i
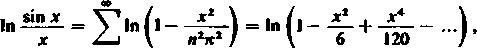
m-l
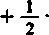
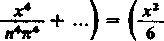
120
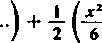
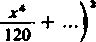
Wyszukiwarka
Podobne podstrony:
386 XII. Ciągi i szeregi funkcyjne Jeżeli dla funkcji /(x) otrzymamy rozwinięcie w szereg potęgowy t
372 XII. Ciągi i szeregi funkcyjne Twierdzenie 1. Niech funkcje u„{x) (n = 1,2,3,...) będą określone
414 XII. Ciągi i szeregi funkcyjne wszędzie ciągłą funkcją zmiennej x. Za pomocą drobiazgowej analiz
430 XII. Ciągi i szeregi funkcyjne Korzystąjąc z rozwinięcia (12) dla dostatecznie małych / mamy ^(—
470 XII. Ciągi i szeregi funkcyjne Dwie kolejne funkcje parzystego rzędu <p2k(z) i <p2k+2{z)
400 (5) XII. Ciągi i szeregi funkcyjne 10) Rozpatrzmy rozwinięcie (dla
448 XII. Ciągi i szeregi funkcyjne 457. Funkcja wykładnicza. Widzieliśmy [404, (11)], że dla dowolne
452 XII. Ciągi i szeregi funkcyjne Naturalne będzie określenie funkcji cos z i sin z dla dowolnego z
464 XII. Ciągi i szeregi funkcyjne Twierdzenie odwrotne nie jest jednak prawdziwe: różne funkcje mog
11233 Strona�3 S 3óó XII. Ciągi i szeregi funkcyjne W drugim przypadku wysokość garbów, które przesz
364 XII. Ciągi i szeregi funkcyjne 428. Zbieżność jednostajna i niejednostajna. Przypuśćmy, że
366 XII. Ciągi i szeregi funkcyjne W drugim przypadku wysokość garbów, które przeszkadzają w
368 XII. Ciągi i szeregi funkcyjne 429. Warunek jednostajnej zbieżności. Twierdzenie
370 XII. Ciągi i szeregi funkcyjne Dla liczby ct [429] znajdziemy taki wskaźnik ą, że
374 XII. Ciągi i szeregi funkcyjne 432. Uwaga o zbieżności ąuasi-jednostajnej. Jeżeli szereg funkcyj
376 XII. Ciągi i szeregi funkcyjne Odejmując tę równość wyraz po wyrazie od (11) łatwo otrzymujemy(1
378 XII. Ciągi i szeregi funkcyjne Tutaj J o więc szereg można całkować wyraz za wyrazem, mimo że dl
380 XII. Ciągi i szeregi funkcyjne w którym suma pierwotnego szeregu nie może mieć pochodnej, gdyż j
więcej podobnych podstron