0430

432

XII. Ciągi i szeregi funkcyjne

spełniają równości (20), które są w pełni równoważne z (18a). Tak więc całe zagadnienie sprowadza się teraz tylko do dowodu, że szereg (19), którego współczynniki wyznaczamy ze wzorów (21), jest zbieżny w pewnym otoczeniu zera.

Rozpatrzmy wraz z (18) analogiczną zależność

(18*) y = y₁₀ x + y₂₀ *²+yn xy + y₀₂ y²+ y₃₀ x³ + y_2l x²y + y_I2 xy² + y₀₃ y³ + ..., w której wszystkie współczynniki y_ik są dodatnie i spełniają poza tym nierówności (22)    \c_ik\ < y_ik.

Skonstruujemy dla niej, na razie formalnie, szereg analogiczny do (19):

(19*)    y = a_k x + a₂ x² + a₃ x³+ ... +a„ x"+ ... ,

przy czym jego współczynniki określimy wzorami podobnymi do wzorów (21):

<*i = 7io .

(21*) a₂ = y₂₀ + y_ily_lo + y₀₂y²o ,

«3 = (Tu +2y₀2 yio)(?2o+yn yio+y₀2 yfo)+y₃o+y2i yio+y,₂ yf₀+y₀3y?o •

Układ tych wzorów, z uwagi na uprzednie rozważania, zapewnia dodatniość liczb a". Prócz tego, po porównaniu ich z (21) i uwzględnieniu (22) widzimy, że dla wszystkich n jest także

(23)    KI < ct„.

Gdyby się udało tak dobrać dodatnie współczynniki y_lk, aby były spełnione nie tylko warunki (22), lecz żeby także odpowiedni szereg (19*) miał różny od zera promień zbieżności, to wobec (23) to samo dotyczyłoby szeregu (19) i twierdzenie byłoby udowodnione. Przejdźmy teraz do wyznaczania liczb y_ik.

Istnieją takie dodatnie liczby /• i p, że szereg podwójny

kiol •'* + |c₂₀| r² + |cnl rp + \c₀₂\p²+ ...

jest zbieżny, a więc jego wyraz ogólny |c_(A.| r'p^k dąży do 0, skąd wynika, że jest on ograniczony :

M

k/fcl • ^r'p^k < M , skąd |c,*| <    .

Przyjmijmy y_ik = M/r‘p^k i zgodnie z powyższym rozpatrzmy zależność

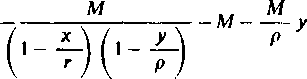
M    M , JW    M ,

y =-x-l--H--xyĄ--- y^l-1-

r    r-    rp    p~

lub wreszcie

p²    Mp² x

p + M    p + M r—x

Okazuje się, że istotnie można znaleźć funkcję y = y (x) spełniającą równanie, a mianowicie tę jej gałąź, która staje się równa 0 dla x = 0. Rozwiązując równanie kwadratowe