0426

428

XII. Ciągi i szeregi funkcyjne

Te właśnie liczby B, nazywamy liczbami Bernoulliego. Pochodzi to od Jakuba Bernoulliego, który pierwszy otrzymał je przy badaniu sum potęg o wykładnikach naturalnych kolejnych liczb naturalnych. Liczby Bernoulliego odgrywąją ważną rolę w wielu zagadnieniach analizy.

Zastępując dla ułatwienia x przez 2x otrzymujemy rozwinięcie

(13) jc ctgh x =

= i -f-    x² —jf¹j_ ... +(-iy-¹    jc^ł-+ ... = 1+V (— l)"-¹ -?"¹!' X²',

2!    4!    (2n)l    Z_i    (2 n)\

R—1

prawdziwe dla dostatecznie małych wartości x.

W 443, 3) mieliśmy już rozwinięcie

00

nx ctgh tix = 1 +2 ^ (—    • x^ln,

1

w którym przez s₂, oznaczona była suma szeregu ^ —ar • Zastępując w równości (13) ¹ przez nx zapi-

1 ^

szemy ją tak:

KX Ctgh TZX = 1+ V (-i)"-¹ (2"⁾²’f" • Z_i    (2«)!

Obydwa rozwinięcia są oczywiście tożsamościowo równe, skąd

B_n

2(2n)! (2tt)²"

a więc wszystkie liczby B_n są dodatnie. Ponieważ dla n -¹■ oo oczywiście s₂„ -»• 1, więc z otrzymanego wzoru wynika, że liczby Bernoulliego rosoą(‘) do nieskończoności wraz ze wzrostem wskaźników.

Po drodze zwróćmy uwagę na pożyteczne wzory na sumy s₂„:

00

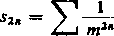
(27t)²* 2 (2n)!

m-1

■B„ ;

w szczególności [porównaj 447, 6)]

oo

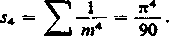
m—1

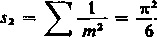
RI—1

Przypominamy sobie teraz, że mieliśmy [443, 2)] już rozwinięcie

(14)    TZX Ctg TtX =1 — 2 S_2n JC²™ ,

R-»l

którego współczynniki też były zależne od sum s_2n. Zastępując tu kx przez x i podstawiając otrzymane za pomocą liczb Bernoulliego wyrażenia na s₂„, otrzymujemy

00

(15)    JKCtg¹ = 1— ^^— x^ln.

Z-I (2/ł)!

n— 1

Ponieważ wiemy, że rozwinięcie (14) zachodzi dla |jc|<1, więc rozwinięcie (15) słuszne jest dla ]jc| <rr. Jednakże, gdy x -¹■ lewa strona równości (15) rośnie do nieskończoności, a więc szereg po prawej

1

Chociaż jak widzieliśmy niemonotonicznie, a według dość kapryśnego prawa.