0436

438

XII. Ciągi i szeregi funkcyjne

Podamy przykłady.

1) Zaczniemy właśnie od wykorzystania wzoru (30). Niech będzie dane równanie

y = x(a+x) (a*0),

czyli

x

y

l

a+x '

Ponieważ

d-¹    1    _ (-iy+^Oi+l) ...(2i>-2)

dx*~^l (a+xY    (a-ł-*)²"^-1

otrzymujemy rozwinięcie

₌ Z. -.

a

(2n—2)    ;

(«—!)!«! a¹

+ ...

To samo rozwinięcie otrzymalibyśmy rozwiązując równanie kwadratowe względem x i wybierając to rozwiązanie, które jest równe 0 dla y = 0.

2) Wyjdźmy teraz od równania typu (25)

y = a+—, y

jest tu więc <p (y) = l/y. Przyjmując f(y) — y~^k, otrzymujemy na mocy wzoru Lagrange’a (29)

ł _ 1    k *² . k(k+^)    x³ . *(*+4) (*+5) x* _k(k+5)łk+6)(k+l'»

f    ^X o‘+^{2 +} 2!    n*⁺⁴    3!    a*+*    ⁺ 4! ’    «*+»

Ponieważ dane równanie sprowadza się do równania kwadratowego:

y¹—ay—x = 0,

więc oczywiście

+ * (*).

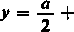
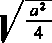
Gdy na przykład a = 2. wówczas otrzymujemy [po pomnożeniu przez 2^k] rozwinięcie

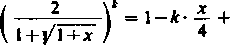
*(*+3)

2!

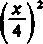
k(k+4) (* + 5) /*\³ 3!    \ 4 /

3) W astronomii teoretycznej ważną rolę odgrywa równanie Keplera

E = M+e sin E,

gdzie E jest anomalią mimoirodową planety, M — anomalią średnią, a t — mimośrodem orbity planety. Korzystając z szeregu Lagrange’a (29a) możemy otrzymać rozwinięcie E w szereg według potęg mimo-środu o współczynnikach zależnych od M

E = M+e sin M+ 4r • -~rs\nⁱM+ ... + ~ •    sin "^M+ -

2! dM    iń dM"~^l

(^l) Znak plus przed pierwiastkiem wybraliśmy dlatego, że dla x = 0 musi być y = a.