0454

456

XII. Ciągi i szeregi funkcyjne

461. Przykłady. W tym ustępie pokażemy na kilku przykładach, jakie korzyści daje zmienna zespolona i jej funkcje elementarne dla analizy funkcji rzeczywistej.

1) Łatwo można wyznaczyć kolejne pochodne funkcji y = l/(*²+1), gdy przedstawimy ją w postaci

y =

2i \ x—i

1

*+i

)■

Mianowicie

y-i ₌    [_1___1_1    .    (—1)"-»(/»—1)!    (*+/)"-(*-/)■

2i    L (*—0"    (jt+i)*    J 2/    (x²+l)“

D! f.., n (n-1) (n-2)    ₃    1

(*² + ł)" L    1-2-3    J'

Na przykład

/    1    V⁴⁾ _{= 24}. 5x*—10x²+l

U² + l/    (*² + l)⁵    '

Tym samym otrzvmujemy oczywiście również kolejne pochodne funkcji arc tg x [porównaj 116,8) i 118,4)].

2) Wzory Eulera wyrażające kosinus i sinus przez funkcję wykładniczą mają różnorodne zastosowania. Gdy chcemy, na przykład, otrzymać zwięzły wzór na sumę

«

s = y cos kx,

możemy to zrobić po prostu obliczając sumę postępu geometrycznego:

i    i

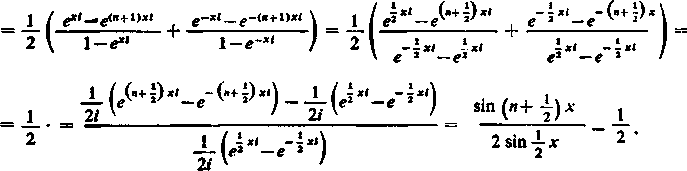
3) Dodatnie całkowite potęgi sin x i cos x, jak również iloczyny tych potęg można przedstawić jako kombinację liniową sinusów i cosinusów wielokrotności argumentu. Łatwo można to zrobić na podstawie wzorów Eulera rozwijając wyrażenia

—-

według wzorów na dwumian Newtona. Na przykład

0-3x1 —    —

0,3x1 — e~^5xt

sin⁵* = -i-(e**'-5e^32,+ 10e*'-10e-^x,-)-5e-32/

16 V

2i

e»*'—e

2i

-3x1    fjcl _    ,

-^+toJLw

_1_

) 16

(sin 5x—5 sin 3*+10 sin x) ;