0400

402

XII. Ciągi i szeregi funkcyjne

Szeregi te można też wykorzystać dla rachunków przybliżonych. Rozpatrzmy dla przykładu szereg

¹ \ - ⁿ (l    ¹___3___5___175___441    \

l/T/ ²\    ⁸    256    2048    262144    2097152    j    '

Jeśli pozostawimy tu tylko wyrazy już napisane, to odpowiedni błąd będzie ujemny; a oto jego oszacowanie;

Ml <

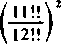
I

11 • 2⁶

< 0,00024 .

Można oczekiwać trzech dokładnych cyfr po przecinku. Rzeczywiście, przeprowadzając obliczenia na liczbach z pięcioma cyframi po przecinku, mamy:

1,35057 <    C 1,35085,

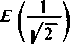
= 1,350 ...

71

2

= 1,57080(—)	TT t 1 2 ' 8	= 0,19635(—)
	TT ^ 3 2 ’ 256	— 0,0I841(~)
1,57080	TC 5	= 0,00383(+)
0,21997	2 2048
1,35083	77 175	- 0,00105(—)
	2 262144
	TT 441	— 0,00033(4-)
	2 2097125
		0,21997

[porównaj 328, 4)].

Należy zaznaczyć, że tylko dla małych wartości k podane uprzednio szeregi dla całek eliptycznych K(k) i E (k) są rzeczywiście wygodne do obliczeń. Istnieją jednak przekształcenia pozwalające na sprowadzenie obliczeń tych całek do przypadku dowolnie małego k [porównaj 315],

14)- Otrzymane rozwinięcie funkcji E (k) można wykorzystać do obliczenia następującej całki:

77/2

/

£ (h sin 0)

1 —h² sin²0

sin 0 dd

(0 <h< 1).

o

n— 1

Przede wszystkim łatwo sprawdzić, że ma miejsce rozwinięcie

mnożąc na przykład prawą stronę równości przez l—k².

Po podstawieniu k = h sin 0 i pomnożeniu przez sin 0 możemy ten szereg całkować względem 0 od 0 do tt/2 wyraz za wyrazem, ponieważ otrzymany szereg jest zbieżny w tych granicach jednostajnie (jego majorantą jest na przykład poprzedni szereg dla k = h). Ponieważ [321 (8)]

(2//)!!

(2/i-ł-l)!! ’

77/2

J sin²ⁿ+^,dd8 = o