0438

440

XII. Ciągi i szeregi funkcyjne

łatwo można wykazać istnienie różnicy i ilorazu, wyrażonych wzorami

(x+yi)-(x’+y'i) = (x-x’)+(y-y') i,

x+yi ₌ xx’+yy' ^ x’y—xy' . x’+y'i x^,2+/²    x'²+y'²

Ostatni wzór jest słuszny przy założeniu, że x'+y'i=ć0, to znaczy, że x'²+y'²>0.

Prócz tego dla liczb zespolonych spełnione są wszystkie zwykłe prawa działań nie związane z pojęciami większy i mniejszy (pojęć tych dla liczb zespolonych nie wprowadzamy). Mówiąc ściślej, spełnione są warunki II1° - 4° z ustępu 3 i III 1° - 5° z ustępu 4.

Wprowadźmy na płaszczyźnie prostokątny układ współrzędnych xOy (rys. 63). Każda liczba zespolona z = x+yi może być wtedy przedstawiona jako punkt M (x, y) tej płaszczyzny, którego współrzędnymi są część rzeczywista i część urojona tej liczby. Oczywiście jest też i na odwrót: każdemu punktowi M płaszczyzny odpowiada w sposób jednoznaczny pewna liczba zespolona. W związku z powyższym rozpatrywaną płaszczyznę nazywamy płaszczyzną zmiennej zespolonej z lub też po prostu płaszczyzną zespoloną.

Liczby rzeczywiste x = jt+0 • i są przedstawione punktami osi x (gdyż dla nich y = 0), a liczby uro-

joneyi = 0-t-y/ (x = 0) punktami osi

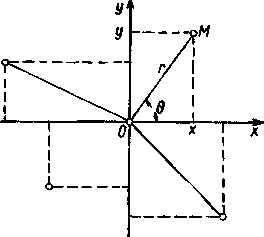
y. Dlatego też pierwszą z tych osi nazywamy osią rzeczywistą, a drugą — osią urojoną.

Ważną rolę spełniają też współrzędne biegunowe r, & punktu, będącego obrazem liczby z = x+yi (patrz rysunek). Nieujemną liczbę r nazywamy modułem lub wartością bezwzględną liczby zespolonej z i oznaczamy r = |z|. Moduł liczby zespolonej wyznaczony jest jednoznacznie przez liczbę z wzorem

ki = ±1■^/x²+y² ,

Jest on równy zeru wtedy i tylko wtedy, gdy z = 0. Kąt & nazywamy argumentem liczby zespolonej z: 6 = Arg z. Dla z=£0 wyznaczamy go z równości

^Ry^s- ^    cos & = --, sin O = —,

r    r

tylko z dokładnością do składnika postaci 2kn (k liczba całkowita). Dla z = 0 argument w ogóle jest nieokreślony. Z wyjątkiem tego przypadku dla każdej liczby z istnieje jeden i tylko jeden argument 0 spełniający nierówność

— 7T < 6 < 7T .

Nazywamy go wartością główną argumentu i oznaczamy przez arg z. Jeżeli 6<ir, to

_tc 0 sin 0    _ r sin 0    y

2 1+COS0 r-rr COS 0 ^— _x +    ’

i kąt arg z można wyznaczyć z równości

arg z = 2 arc tg..............

x + yx²+y²

Równość tę można stosować dla wszystkich liczb zespolonych oprócz liczb rzeczywistych ujemnych i zera.

Zauważmy, że moduły liczb zespolonych z = x+yi i z' = x'+y‘ i też spełniają nierówność

|r+z'| < |z| +|z'|,