0394

396

XII. Ciągi i szeregi funkcyjne

Analogicznie rozwijając w szereg pochodną

[ln u+yT+7*)]' - —-1—

ł/l+JC²

i całkując wyraz za wyrazem otrzymujemy rozwinięcie

ln (x+y'l+x²) = x+

(2/i —1)!1 " (2/0!!

x^2m+l

2n+l

(-1 < X < 1).

Jest to Arsinh x, tzn. funkcja odwrotna do sinh x [49, 4); 339, uwaga].

4) Przez całkowanie szeregów wyraz za wyrazem otrzymujemy rozwinięcia w szeregi nieskończone potęgowe pewnych całek, nie dąjących się przedstawić za pomocą funkcji elementarnych w postaci skończonej [patrz 272]. Rozwinięcia te można wykorzystać do obliczeń przybliżonych.

Na przykład wychodząc ze znanego rozwinięcia

! ‘ 2!

-... +(-l)"^—+ ... nl

[porównaj 404 (11)] otrzymujemy

I ^e

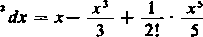
+(-i r-V

n\

x^ł"^łl

2/i+l

Rozwiążmy teraz następujące zadanie: obliczyć całkę

1

W= f e-^x*dx

O

z dokładnością do 0,0001. Biorąc granicę górną całki równą 1, otrzymamy dla W szereg liczbowy naprzemienny

1-T + -TT 3    10

1

42

+

216

1320

1

9360

1

75600

+

Ponieważ ósmy wyraz rozwinięcia jest już znacznie mniejszy niż zadany stopień dokładności, więc pozostawimy tylko pierwszych osiem wyrazów. Odpowiedni (ujemny) błąd A daje się łatwo oszacować

Mi <

1

75600

<

1,5 10⁵ '

1	= 1,10000	1
10		3
1	= 0,00463 (-)	1
216		42
1_ 9360	= 0,00011 (-)	1 1320

1,10474

Obliczamy pozostałe wyrazy biorąc pięć cyfr po przecinku

1 +

1U    J

1,10474

0,35790

0,74684

= 0,02381 (-) = 0,00076 (-)

0,35790

Gdy uwzględnimy wszystkie błędy, wówczas otrzymamy

0,74681 < W < 0,74685, W = 0,7468...

z dokładnością do czwartego miejsca po przecinku [porównaj 328, 5)]. 5) Analpgicznie, ponieważ [porównaj 404, (12)]

— + — 3!    5!

... +(-!)"

X²"-²

(2/i—l)!