5125715739

3. Przystawanie trójkątów 15. Na bokach AB, BC i CA trójkąta równobocznego ABC leżą odpowiednio punkty D, E i F tak, że AD = BE = CF. Udowodnij, że trójkąt DEF jest równoboczny. Rozwiązanie. Ponieważ AD = BE = CF i AB = BC = CA, więc DB = EC = FA.

Teraz zauważamy, że AADF = ABED = AC FE (cecha przystawania BKB), skąd wynika, że DE = EF = FA.

16. Na bokach BC i CD równoległoboku ABCD zbudowano (na zewnątrz równole-głoboku) trójkąty równoboczne BCK i DCL. Udowodnij, że trójkąt AKL jest równoboczny.

Rozwiązanie. Przypuśćmy, że kąt a jest kątem ostrym równoległoboku oraz a < 60°. Pozostałe przypadki pozostawimy jako ćwiczenie.

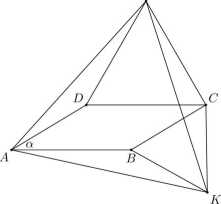
Wówczas AB — LD — LC oraz BK - DA — CK. Ponadto

IABK = 360° - LABC - 4.CBK = 360° - (180° - a) - 60° = 120° + a, LLDA = 360° - Z.ADL - ILDC = 360° - (180° - a) - 60° = 120° + a, 4.LCK = LBCD + ĆBCK + ZLCD = a + 60° + 60° = 120° + a.

Wyszukiwarka

Podobne podstrony:
str130 stałego. Pasy wyznaczone przez pary tych prostych ab, bc, ca oraz Im, mn, nl odpowiadają ścia
12. Na bokach AC i BC trójkąta ostrokątnego ABC zbudowano, na zewnątrz trójkąta, dwa trójkąty równob
slajd154 (2) Na danej płaszczyźnie a wyznaczyć rzuty trójkąta równobocznego ABC, którego bok AB
Creat0007 TIF 58 Wiadomo, że stąd U =u =U =U • b c fu =u =u =u ab bc ca U=2 U • cos30 U=V3 • U (6.3
geometria anlityczna 2 podstawa 46. Punku- A = 11.-2). C = {4.2) są dwoma wierzchołkami trójkąta rów
Zadanie 22. (1 pkt) Punkty -4 = (-5,2) i B = (3,-2) są wierzchołkami trójkąta równobocznego ABC. Obr
skanuj0052 Dana jest płaszczyzna a=ABK. Wyznacz rzuty trójkąta równobocznego ABC zawartego w płaszcz
Obrazek32 Zadanie 26. (5 pkt) Prosta /: 3x+ 2y- 21 = 0 zawiera wysokość trójkąta równobocznego ABC.
11. Trójkąty równoboczne ABC i BDE są położone tak, że punkt B leży
9. Punkty D, E, F leżą odpowiednio na bokach BC, CA, AB trójkąta ABC. Okręgi wpisane w trójkąty AEF,
e trapez Zad.20 Oblicz pole trójkąta ABC opartego na wektorach AB = m + 5« i BC = 4m + 3/?, wiedząc,
" 0 Na bokach trójkąta prostokątnego zbu-^wano trójkąty równoboczne w sposób rZedstawiony na ry
8. Punkt O jest środkiem okręgu opisanego na trójkącie ABC. Punkt K leży na b
33 W tym celu dzielimy AQ, QC, AB i BC, powiedzmy, na 10 równych części, a wtedy dla — - 0,1 mamy: —
2. Nierówność trójkąta 13. Punkty K i L leżą na boku AB trójkąta ABC. Udowodnij, że obwód trójkąta K
FINAŁ XII Olimpiada Matematyczna Juniorów Zadanie 2 Punkt D leżu na boku AB trójkąta ABC. Pdnkt E le

więcej podobnych podstron