Creat0007 TIF

58

Wiadomo, że

stąd

U =u =U =U

• b c f

u =u =u =u

ab bc ca

U=2 U • cos30' U=V3 • U

(6.3)

Dla symetrycznego odbiornika funkcje prądów możemy

#

przedstawić:

i =1 •sin(wt-f) a m	(6.4a)
i =1 •sin(wt-120^#-p) b ■	(6.4b)
i =1 *sin(wt-240°-f) ca	(6.4c)
u	•
i - * m Z	(6.5)

przy czym gdzie:

, f>=0

o<f><n/2

»»=n/2

n/2<f><o

©=-n/2

impedancja każdej fazy odbiornika,

kąt fazowy    impedancji,    przyjmujący

wartości:

obciążenie rezystancyjne, obciążenie o charakterze indukcyjnym, obciążenie indukcyjne,

obciążenie o charakterze pojemnościowym, obciążenie pojemnościowe.

• / •

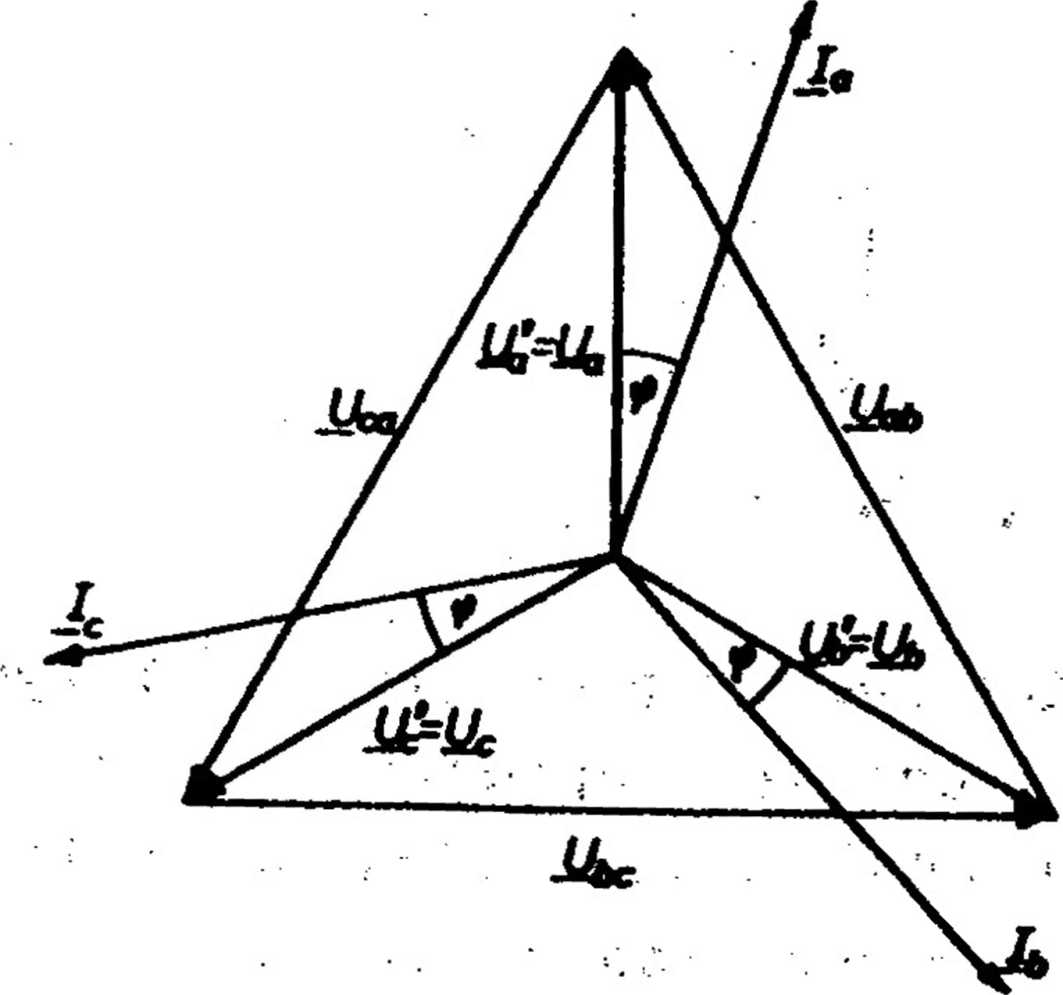
Wykres wektorowy napięć i prądów symetrycznego odbiornika trójfazowego połączonego w gwiazdę

■* V

Rys.6.3.

Wartości skuteczne prądów będą sobie równe (I =1=1 =1).

Moc czynna pobierana przez odbiornik symetryczny Jest równa trzykrotnej mocy Jednego odbiornika.

(6.6)

P=3«P_f=3*U_f•3•cos?

U

ponieważ

V

I

to

U

•U* I *COSf>

2

(6.7)

lub

•COS?

(6.8)

Dla odbiornika symetrycznego nie ma znaczenia_r dodatkowe połączenie pomiędzy punktem zerowym sieci i punktem gwiazdowym odbiornika. Ma ono natomiast istotne znaczenie w przypadku odbiornika niesymetrycznego    W    układzie

trbjprzewodowym obciążonym niesymetrycznie na każdym z odbiorników występują różne napięcia. Potencjał punktu gwiazdowego odbiornika nie leży w środku trójkąta napięć

-V

niędzyfazowych. Pomiędzy punktami zerowymi sieci zasilającej 1 odbiornika występuje różnica potencjałów U .

O

Rys. 6. 4. Wykres wektorowy napięć i prądów niesymetrycznego

odbiornika trójfazowego połączonego w gwiazdę