5125715750

Ponieważ trójkąt FE A jest równoramienny (z założenia mamy F A = EA), więc

LAFE = LAEF =

180° - a 2

a

2'

Podobnie trójkąt DFB jest równoramienny, skąd wynika, że

P

2'

LBFD = LBDF = 90°

Stąd dostajemy

IEFD = 180° - (90° -

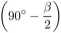
a+/3    180°-7 „„„    7

2 ^_ 2 2'

5. W pięciokącie wypukłym ABC DE poprowadzono wszystkie przekątne. Oblicz sumę kątów LCAD + /.DBE + LECĄ + LADB + LBEC.

Rozwiązanie. Niech P i Q będą punktami przecięcia przekątnej AD odpowiednio z przekątnymi BE i CE. Oznaczmy kąty literami greckimi tak jak na rysunku:

D

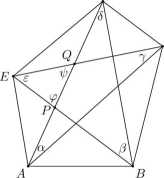
Kąt <p jest kątem zewnętrznym trójkąta BDP, a więc <p = 0 + S. Kąt tp jest kątem zewnętrznym trójkąta ACQ, więc ip = a + 7. Suma kątów trójkąta PQE jest równa V? + ip + £ = 180°, skąd wynika, żea + fi + 'y + S + £= 180°.

6. Dany jest czworokąt wypukły ABCD. Punkty P, Q, R i S są punktami przecięcia dwusiecznych kątów zewnętrznych czworokąta ABCD. Udowodnij, że sumy przeciwległych kątów czworokąta PQRS są równe.