5672968843

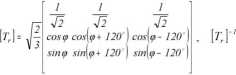
Ji

coscp

cos[ę + 120 ) cos[(p- 120)

sin ę

sin[<p + 720 ) . sin[<p- 120 ) (3.8)

Po transformacji równań wirnika równania różniczkowe stojana i wirnika mają postać

i A

d

W A

0

00 0

^UB

ł -dt

Wb

0

= Rr

ini

d + —

Wru

-

00-1

Wru

Ur

^1C

Wc

0

Wru

0 1 0

Wrv

a wyrażenie momentu elektromagnetycznego

	0 0 - I
\h '« 'cl'	n ^1		r0
	0 — -2 2		iru
	„21 i		in

(3.10)

Po dokonaniu transformacji otrzymuje się równania strumieni skojarzonych z uzwojeniami stojana

V A		1 1 ^LcS ^+ ~^lm ~^L.\I 1 . , „ 1		iA	[3.	0 1 0 1 fi		ir0
V B	^=	— Lu L,*+Lu —Lu 2 " ’ " 2 "		iB	^+	0 - - — 2 2		in
V c		- L,s t i„		*c		o-i-£		in,
		2 2 J				2 2

oraz wirnika

Wrą	fT	0 0 ,-L 2	0		j		L„r 0 0		Ko
Wru			1 ’ 2		^,B	*	0 | Lu + L„ 0		iru
Wru			fi		’c		0 0 -Lu + L		in
		2	2				2 '

(3.11).

(3.12)

Po wprowadzeniu wyTażeń strumieniowo-prądowych (3.9 i 3.12) do równań różniczkowych napięciowy ch (3.10) otrzymuje się równania napięciowe dwu zastępczych obwodów klatki wirnika

12