5783291265

Kinematyka

Kinematyka

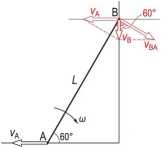
Rys. 2.3.

kierunek prędkości u_B

Prędkość względną i>ba określamy następująco: i»ba =a-L

gdzie prędkość kątowa pręta co jest niewiadomą.

Na rysunku 2.3 przedstawiono schemat obliczeniowy. Jeżeli zrzutujemy wektory w punkcie B, na kierunek prędkości i>b i kierunek prostopadły do niego, to otrzymamy następujący układ równań:

jv _B = v_BaCos(60^o)

[- v_A + Vba sin(60°) = 0

Z drugiego równania wyznaczamy vba i podstawiamy do równania pierwszego:

y_BA —----

sin(60°)

= . ^v* cos(60°) = va ctg (60°) sin(60°)

vb

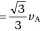
Dodatkowo możemy wyznaczyć prędkość kątową a :

^va _ 2-y/3 v_A Lsin(60°)    3 L

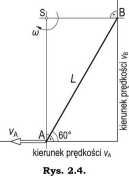
Metoda III

Kolejnym sposobem rozwiązania zadania jest metoda chwilowego środka obrotu. Punkt ten, w rozpatrywanym zadaniu oznaczony jako S (rys. 2.4), znajduje się na przecięciu prostych prostopadłych do kierunków prędkości w punktach A i B.

Prędkość kątowa co jest równa:

Lsin(60°)

a prędkość punktu B wynosi:

Vb = co ■ Lcos(60°) =

Lsin(60^c

V3„

• Lcos(60°) = y_Actg(60°)

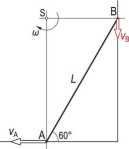
Rys. 2.5.