628033440

można doprowadzić dę postaci:

.K

go

w₃ = _Tp

t₁₊t₂

K

H /s/S r' ¹

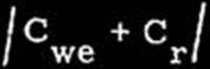
li-

HoCo/K₀n/

go

K ³ O

O

we

/16/

K = O

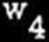
/17j/

/17k/

gdzie:

R

R R

g = 1 + ~y- +    —/K +1/ „ _ ,

^eo    R R R ¹ o ¹ fi 7a/

W zależnościach /17/ użyto czynniki wprowadzone poprzednio oraz dodatkowe:

we co

R = R • C_D o o R

/I8a/

o R C K 0 0 0

- T.-T.-R C +K /T_r -fTcC/

1    2 wy o o

/l?b /

C = C + C r s wy

/ 18b/

1 R C K

o o o

K

V ^{+ T}3^TH ⁺ V* o    o

W celu opisania składowych odpowiedzi rzeczywistego integratora należy wyznaczyć współczynniki wchodzące w skład zależności /6/,/7/, / 8/ i /9/« Dla pierwszych trzech zależności wynoszą one;

R C /K +1/

r =.-?■ ?■    °-    /19/

/^T, ^{+ T}o/- R c R C L

'    1    2/ o o wy s I

R C K o o o

K

/ 20/

^T1^T2 ⁺I^T1 ^+t2/

R    ⁺ R

c    we

/^Twe ^{+ T}W

+ T,

R /

WY I

^a2

TT T_^ T + T R 3    »    12

wy f we

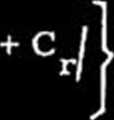
/17c/

o R C K o o o

K_q/^tr + T*/.T -T .

R C o o

K

R / R o

V

R

T,T *

+C R s o	R K
	o 0
TnR
1 wy	^tzI^tr *^t,I
k R
•o o	^r A
- TT R	T./-C„ + C
1 2	wy P/ Ro

/IM/

/IM?

/17f/

- R cl

wy oj

Aby obliczyć współczynniki wchodzące w skład równania /9/ konieczne jest obliczenie biegunów członu:    <

clk<

^Hr2 / ^s/ ⁼    -

w = 1

O

/Iłg/

^T!^+T2 ₊

^W1 ' KO 3

/IM/

w =T^ T

TT T +T

12.1 2

R

K

K

R^W

O

R    1

-22- /T + To / 1+ r?— R /c +c/-„₁₍ R ' we P ' I K wy⁷ we r' /I7i/ we    Jo

a następnie rozkład tego wyrażenia na ułamki proste.

Ustalenie rozmieszczenia biegunów transmin tancji sprowadza się do analizy pierwiastków wielomianu, tworzącego mianownik transmi-tancji. W przypadKU wielomianów stopnia wyższego niż 2 jest to zagadnienie dosyć trudne rachunkowo, zwłaszcza w razie występowania pierwiastków zespolonych.

Przy analizie transmłta-ncji H^/s/zacho-dzi konieczność zbadania wielomianu 4 lub 3 stopnia. Rozwiązanie równania 3 stopnia można oprzeć na wzorach C^rdana, natomiast efektywne rozwiązanie równania 4 stopnia wymaga zastosowania maszyny matematycznej i wykorzystania metod numerycznych. W przy-

7