6790847369

B. Jackowski: Grafika dyskretna 19

ciąg podany w poprzednim punkcie zapisać jako ciąg zaledwie 38-bitowy, czyli 5-bajtowy:

(iii)(m)(iii)(m)(o)(o)(o)(iii)(iio)(iii)(io)(io)(io)(io)(io)(io)(io)

Nawiasy oczywiście nie są częścią kodu wynikowego, zostały pozostawione jedynie dla podkreślenia podziału.

255 (000) 127 (001)    63 (110)    0 (111)

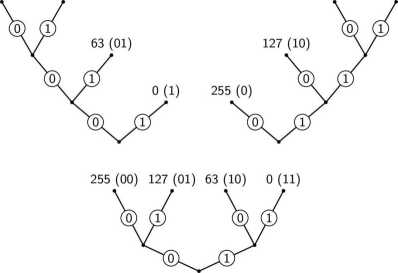
Rys. 7. Załóżmy, że w naszym strumieniu danych wejściowych występują jedynie cztery liczby, na przykład 0, 63, 127, 255. Dowolne drzewo binarne mające cztery zakończenia daje nam możliwość przypisania jednoznacznych zero-jedynkowych kodów tym liczbom: gałęzi idącej w lewo przypisujemy wartość 0, gałęzi idącej w prawo - wartość 1. Liczby umieszczamy w zakończeniach gałęzi i przypisujemy im ciąg cyfr dwójkowych (na rysunku podany w nawiasach), jaki otrzymuje się idąc od czubka drzewa do zakończenia gałęzi.

Wynik kompresji jest lepszy niż w poprzednim punkcie - i jest regułą, że kompresja Huffmana jest bardziej efektywna niż kompresja RLE, ale też mniej wygodna w implementacji.

Znaczącą kompresję uzyskaliśmy, mimo iż jeszcze nie zrobiliśmy użytku ze spostrzeżenia poczynionego na wstępie - im częściej występuje dana wartość, tym krótszy kod zero-jedynkowy powinien zostać jej przypisany.