6800810034

Elementy geodezji wyższej i astronomii.

przy równomiernym rozmieszczeniu mas w skorupie ziemskiej także regularną. Bryła taka to sferoidą. Dużą niedogodnością jest skomplikowane równanie matematyczne opisujące ją. Jednocześnie tylko teoretycznie masy Ziemi są rozłożone równomiernie, a powierzchnie mórz są spokojne i o jednakowej gęstości.

Bryła powstała przy przyjęciu średniego poziomu mórz i oceanów przedłużonego pod lądami i nad depresjami z pominięciem założenia równomiernego rozłożenia mas Ziemi to geoida. Jej powierzchnia nie jest regularna, a linie pionu (kierunki siły ciężkości) odchylają się od linii prostopadłych (normalnych) do sferoidy poprowadzonych przez te punkty.

W miejscach odchyleń pionu powierzchnia geoidy również odchyla się od powierzchni sferoidy. Ze względu na nieregulamość powierzchni nie można napisać równania geoidy.

Brak matematycznego wyrazu geoidy oraz zbyt skomplikowane równanie sferoidy przemawia za przyjęciem do celów praktycznych jako przybliżenia kształtu Ziemi takiej elipsoidy obrotowej, której objętość jest równa objętości geoidy, a suma h odchyleń powierzchni brył najmniejsza. Jest to elipsoida ziemska.

Wszystkie przekroje elipsoidy ziemskiej płaszczyznami przechodzącymi przez oś biegunową są jednakowymi elipsami. Płaszczyzny tych przekrojów to płaszczyzny południkowe, a elipsy będące śladami przecięcia tych płaszczyzn z powierzchnią elipsoidy to południki ziemskie. Przekroje elipsoidy ziemskiej płaszczyznami równoległymi poprowadzonymi prostopadle do osi biegunowej są kołami, których środki leżą na jednej osi. Okręgi tych kół to równoleżniki. Największy z równoleżników, przecinający oś biegunową w połowie to równik.

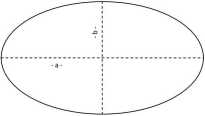
Elementami elipsoidy ziemskiej, występującymi najczęściej w obliczeniach geodezyjnych są: a - półoś duża, b - półoś mała, p - (a-b)/a - spłaszczenie,

e² = (a²-b²)/a² - pierwszy mimośród (ekscentryczność),

(e’)² = (a²-b²)/b² - drugi mimośród (eliptyczność).