7292100830

470 Rachunek wyrównawczy.

Związki te naz. równaniami poprawek, zaś spółczynniki nieoznaczone k korelatami. Rugując poszczególne o w równaniach odchyłek (l) przy pomocy równań poprawek (5), otrzymujemy r równań korelat:

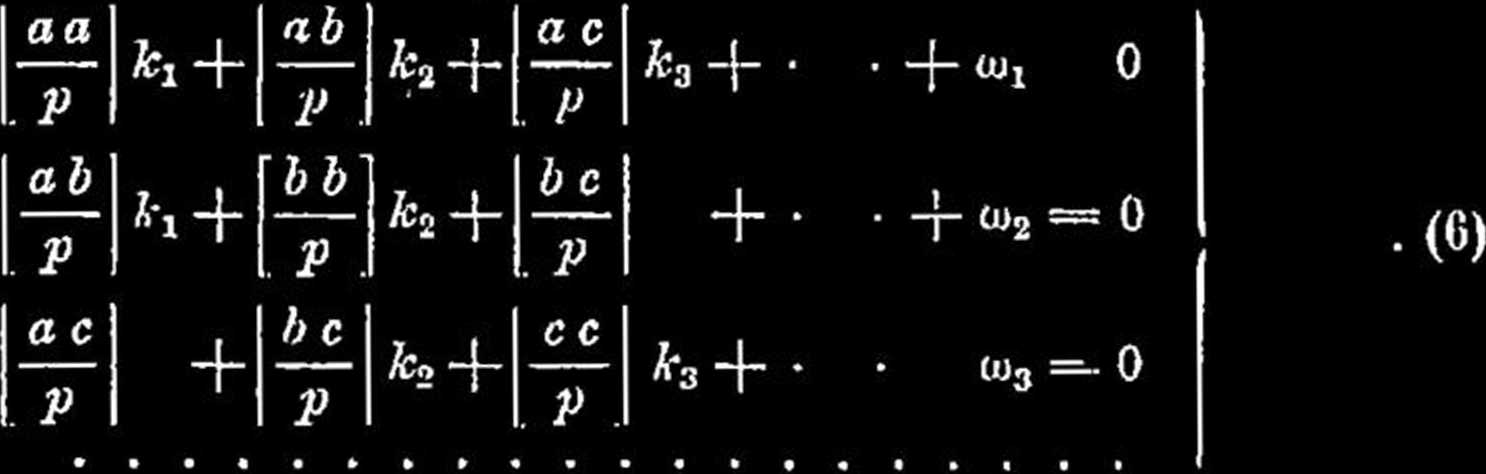
Po rozwiązaniu równań korelat, które przeprowadza się annlogiczneini sposobami, co rozwiązanie równań normalnych, wstawia sic wartości do równań poprawek (5), uzyskując ich wartości.

Jednostkowy błąd średni: ja*,

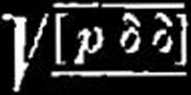
zaś błędy średnie poszczególnych spostrzeżeń (przed wyrównaniem): u.. =

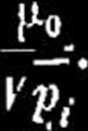
Błąd średni funkcji wyrównanych spostrzeżeń

określa wzór:

		^Ł'.l p		^Cf P
		^bbA P

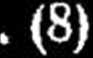
przyczem f.

Jeżeli mamy wyznaczyć błąd średni spostrzeżenia wyrównanego, tj. należy zastosować wzór (8), przyjmujący)— 1, zaś resztę f—0.

Zamiast posługiwać się metodą opisaną, można sprowadzić wyrównanie spostrzeżeń za warunkowanych do wyrównania spostrzeżeń pośrednich. Wybieramy oczywiście te metodę, która nastręcza mniej pracy rachunkowej.

Ponieważ n > r, wybieramy (n — r) niezależnych poprawek, zawartych w równaniach (l), a oznaczywszy je przez y, z,    usta wda my w równań

błędów o (n — r) — k niewdadomych; wyrównanie przeprowadzamy następnie wedle str. 467, przyczem niewiadomemi jest owych (« — r) — k niezależnych poprawek o.

O wyborze metody wyrównania decyduje w pierwszym rzedzie, czy

a) (n — r) > r lub u > 2 r,    b) (n — r) = r lub n = 2 r,

c) (» — »•) < r lub w ■< 2 r.

W przypadku o) posługujemy się przy wyrównaniu metodą korelat, w przypadku c) metodą spostrzeżeń pośrednich; jeżeli (» — r) = r, decydują o wyborze inne w^rzględy, jak obliczenie wag, wyrazów wolnych itp.

Przykład wyrównania spostrzeżeń zawarunkow^Tanych por. str. 420.

LITERATURA.

K. Weigel: Rachunek wyrównawczy. Lwów—Warszawa 1923.

H. Poincaró: Calcul dee Grobalitós. Paria 1912.

E. Czuber: Theorie der Bcobaciitung8fehler. Loipzig 1891.

Helraert: Ausglelchungsrechnung n. d. Methodo d. kl. Quadrafce. 1907. Jordan: Tom I. (por. sir. 466),

Wellisch: Theorie und PraxJs der AuagleichBrecbnung. 1909.

132