7483798794

b.    Policz wydajność pracy i wskaźnik zatrudnienia (czyli miarę wykorzystania zasobu pracy) dla każdego kraju. Jakie wnioski możesz wyciągnąć z porównania?

c.    Przyjmując kraj 1 jako podstawę porównań (benchmark) policz lukę PKB per capita krajów 2 i 3 jako procent PKB per Capital kraju 1 i zdekomponuj te lukę na część wynikającą z różnicy wydajności pracy i różnicy w wykorzystaniu populacji w procesagch wytwórczych.

2.    Rozważ funkcję produkcji postaci Y(K, L) = K2L2

a.    Sprawdź czy funkcja produkcji ma stałe korzyści skali.

b.    Oblicz poziomy produkcji dla par (K,L):( 1,1), (2,1), (3,1), (1,2), (1,3). Czy dla rozważanego zakresu zmienności czynników produkcji przychody z kapitału są malejące? A przychody z pracy? Jakie to może mieć konsekwencje dla rozwoju krajów wysoko- i niskorozwiniętych?

3.    Dany jest wykres poniżej:

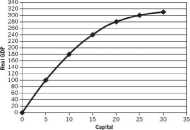
a.    Jak jest krańcowy produkt 5 jednostki kapitału (czyli zwiększenia ilości kapitału z 4 na 5)?

b.    Jak jest krańcowy produkt 10 jednostki kapitału (czyli zwiększenia ilości kapitału z 9 na 10)?

4. Uzupełnij brakujące pozycje w tabeli, która pokazuje liczbę obsługiwanych w trakcie godziny klientów w zależności od liczby zainstalowanych kas.

Liczba    Liczba Produkt

kas w    obsłużonych    krańcowy

sklepie    klientów    i-tej kasy

0	5
1	20 15
2	12
3	42
4	48 6
5	2

5. Niektóre dane mogą być zastanawiające na pierwszy rzut oka. Przykładowo, udział PKB przeznaczany na inwestycje w latach 1960-1990 w USA i Korei Południowej był zbliżony, a jednocześnie Korea Południowa rosła w tym okresie przeciętnie o ok. 6% rocznie, a USA

2