8377355047

dwu dźwigarowego z pracującym pokryciem na omegówkach według [8].

Najnowszy polski bombowiec PZL — 37

/\/s»s/wv/\/s/s/v^/s^\^s/s/s^s

	Wiel kość spółczy unik a K
Pracujący element	na ściskanie	na rozciąganie
Pasy dźwigarów......	1,0	1,0
Podłużne omegówki między dźwigarami lub w przedzie skrzydłu......	0,5	0,75
Podłużne omegówki w tylnej części skrzydła z powodu tego. że tylna część skrzydła pracuje wogóle słabo i jest przecięta klapą i lotką........	0,0	0,0
Pokrycie od przodu do tylnego dźwigara.....	K	0,75

gdzie:

5

E

<*[>!

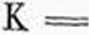
nanie przy pewnym rozkładzie momentów zginających wzdłuż rozpiętości skrzydła. Jednakże nie liczymy odrazu na momenty zginające niszczące, lecz „obliczeniowo" stopniowo obciążamy keson momentami zginającymi tzn. dzielimy zakres od zera do „n" niszczącego na pewną ilość części, które będziemy nazywali przez „ni", „n₂“ ild. aż do „n“ niszczącego. Znachodzimy geometryczny środek ciężkości przekroju i obciążamy momentami zginającymi n,, n₂..., obliczając przy tym największe naprężenia rozciągające i ściskające. Przy pewnym „m" naprężenia ściskające w pokryciu przekroczą naprężenia krytyczne i część strefy ściskanego pokrycia na pewnym luku o kącie środkowym ulegnie sfał-dowaniu i praktycznie przestaje pracować w lOOtyo. Trudno dokładnie określić, od czego to zależy. W skrzydle względnie w kesonie, nawet w granicach sprężystych odkształceń, naprężenia lokalizują się w bardziej sztywnych elementach. Ta różnorodność rozkładu naprężeń jest spowodowana różną wielkością odkształceń wskutek miejscowych wyboczeń, mniej sztywnych części pokrycia i usztywnień wzdłużnych. Zatem od pierwszej chwili pracy do momentu złamania nie każdy element przenosi takie naprężenie, jakie mógłby przenieść ze względu na swój przekrój. Zachodzi to dlatego, że nic wszystkie pracujące elementy udaje się rozłożyć w przekroju tak, aby powstające w nich naprężenia odpowiadały icli zdolnościom pracy, dalej z powodu nieznajomości dokładnego prawa rozkładu naprężeń w przekroju itp. Ażeby ten fakt nie-jednostajności pracy poszczególnych elementów ująć liczbowo, wprowadza się pewien spółczyn-nik redukujący, przez który trzeba mnożyć powierzchnie przekrojów i naprężenia elementów mniej sztywnych. Otrzymujemy w ten sposób pewne powierzchnie „obliczeniowe". Wielkości tych spółczynników, (podawane np. przez autorów sowieckich na podstawie doświadczeń), zależą od tego, czy obciążenie zawiera się w granicach sprężystości materiału, czy też jest obciążeniem łamiącym. Zwykle liczy się na obciążenia łamiące. Poniżej podaję wielkość tego spólczyn-nika redukującego „K" dla skrzydła duralowego,

W ielkość K dla pokrycia na powierzchni ściskanej wyznacza się w sposób następujący: Pokrycie na ściskanie pracuje tylko w sąsiedztwie usztywnień wzdłużnych. Nazwijmy przez „c" odległość 2 rzędów nitów od siebie, przytwierdzających pokrycie do omegówki, to na ściskanie pracuje szerokość pokrycia równa:

b=b₀+c......(3)

Dodatkową szerokość „b₀ “ polecają obliczać z wzoru Karman’a, który Lundkwist [11) przedstawia w postaci:

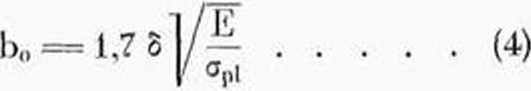
grubość pokrycia,

moduł elastyczności,

granica plastyczności tworzywa.

Dla duralu:

E = 700 000 kG/cm⁸ a , = 2 700 — 2 888 kG/cm⁸ D₀= oo 27 o

Dla sklejki bakelitowej możemy przyjąć z dużym przybliżeniem, że a,,i = a niszczące. Dla takiej sklejki średnio można przyjąć:

E = oo 90 000 kG/cm⁸ <7nisz = l 200 kG/cm* bo = co 13 5.

Oznaczając przez „i" ilość oinegówck na części ściskanej, mamy sumaryczną szerokość pracującego pokrycia:

B = i (b₀ + c).....(5)

otóż spółczynnik „K" wynosi

0,5 i (l)„ + c)

H

gdzie:

II całkowita szerokość ściskanej partii skrzydła. Dla skrzydeł drewnianych, krytych sklejką, można również dla listew przyjąć te same wielkości spółczynników za wyjątkiem

o

T-

272