Temat : CZWÓRNIK

1 WSTĘP.

Czwórnikiem nazywa się część obwodu elektrycznego mającego dwie pary zacisków . Spełnia on rolę pośredniego ogniwa przy przesyłaniu energii elektrycznej między źródłem a odbiornikiem .

Czwórniki mogą być klasyfikowane ze względu na cechę liniowości elementów wchodzących w ich skład, również ze względu na schematy połączeń wewnętrznych np. czwórniki typu T,X,Π. Czwórnik nazywa się pasywnym, jeżeli dla dowolnej chwili t energia pobierana przez czwórnik z układu zewnętrznego jest nieujemna.

Celem ćwiczenia jest wyznaczenie parametrów czwórnika, które pozwalają analitycznie powiązać i zanalizować napięcia i prądy na jego zaciskach.

Schemat czwórnika :

I₁ I₂

1 2

U₁ U₂

1' 2'

2 POMIARY I OBLICZENIA.

a. Wyznaczenie impedancji wejściowej rozwarciowej Z_lj i zwarciowej Z_lz.

A W

I₁ 1 2

U₁ V I_c

1' 2'

U[V]		I[mA]		P[W]
KONDENSATOR TAK NIE		KONDENSATOR TAK NIE		KONDENSATOR TAK NIE
24	20	340	540	1.5	7.45
23	19	320	510	1.35	6.55
22	18	310	480	1.25	6.05

Moc czynna wejściowa czwórnika w stanie jałowym na wyjściu wynosi :

P_j = Re {U₁I₁ I₂=0} = U₁⋅I₁⋅ cosϕ_ljI₂=0

kąt :

moduł impedancji :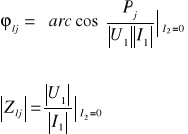

• wyznaczenie impedancji wejściowej rozwarciowej :

Z_lj = 24/0.34=70.58 Ω

ϕ_lj = -arccos(0.018)=-1°23'

Z_lj =70.58 e ^-j1°23'

• wyznaczenie impedancji wejściowej zwarciowej :

Z_lz = 20/0.54=37.03 Ω

ϕ_lz = -arccos(0.69)=0°48'

Z_lz = 37.03 e ^-j0°48'

2. Wyznaczenie parametru C czwórnika .

V	mA	W
10 11 12	180 200 220	1.05 1.3 1.55

I₁

A W 1 2

E V U₂

1' 2'

ΔU

Watomierz wskaże wartość:

W₁ = Re {U₂I₁ I₂=0} = U₂⋅I₁⋅ cosγI₂=0

kąt :

γ=±arc cos (W/U₂∗I ₁ )= 57^O58'

moduł parametru C :

C=I₁ /U₂_I2=O=O.O16

czyli : C =0.016 e ^j57°58'

3. Wyznaczenie parametru B czwórnika.

A W

1 2

E V U₁ I₂

1' 2'

V	A	W
9 8 7	160 140 120	1,4 1,1 0,85

Watomierz wskaże wartość :

W₂ = Re {U₁I₂ u₂=0} = U₁⋅I₂⋅ cosβu₂=0

kąt :

β=± arc cos (W₃ /U₂ ∗I₃)= 29 °85'

moduł parametru B :

B=U₁/I₂U₂=0 =64.28

czyli : B =64.28 e ^j29°85'

4. Wyznaczenie parametrów A i D.

Z_lj=A/C ⇒ A=Z_lj∗C= 1.13 e^j56'35

Z_lz=B/D ⇒ D=B/Z_lz= 1.74 e^j30'33

5. Sprawdzenie symetryczności i pasywności czwórnika.

Czy A=D ? 1.13 e ^j56°35' =1.74 e ^j30°33 A ≠ D

Czy AD - BC = 1 ?

1.13 e ^j56°35 ⋅ 1.74e ^j30.33° - 64.28 e ^j29°85' ⋅ 0.016 e ^j57°58 = 1

L = 0.1 + j1.95 - 0.05 - j1.03 = 0.92e ^j86'53

L ≅ P

3 WNIOSKI.

Otrzymany wynik dla warunku pasywności odbiega nieco od jedynki. Przyczyną mogą być : niedokładność urządzeń pomiarowych, jak również błąd odczytu skali. Wynik ten jednak pozwala stwierdzić, iż badany czwórnik jest odwracalnym. Ponadto stwierdzamy, że badany czwórnik jest symetryczny.

Z przeprowadzonych pomiarów otrzymaliśmy następujące parametry czwórnika :

A = 1.13 e ^j56°35' B = 64.28 e ^j29°85' C = 0.016 e ^j57°58' D = 1.74 e ^j30°33'

---