Zalety CPS: 1.Gwarantowana dokładność, zależy tylko od liczby bitów;2.Perfekcyjna powtarzalność. Nie ma zmian wywołanych tolerancją elementów;3.Nie występuje dryft temperaturowy ani skutki starzenia;4.Postęp w technologii półprzewodników ,uzyskanie większej niezawodności, mniejszych wymiarów, niższych kosztów, niższy pobór mocy i większa prędkość;5.Większa elastyczność, sys. CPS można oprogramować i przeprog.,b y uzyskać różne funkcje bez modyfikacji sprzętu;6.Lepsze charakterystyki, Można realizować funkcje nieosiągalne w tech. analogowej np. liniowe char. fazowe, zespolone algor.filtracji;7.W pewnych przypadkach informacja może być dostępna tylko w postaci cyfrowej i jedyną możliwością jest przetwarzanie cyfrowe;

Wady CPS: szybkość i cena, niskie f<100MHz, czas projektowania, problemy ze skończoną długością słowa.

NyquistaTw.o próbkowaniu: Jeżeli mamy dyskretny ciąg X_C(nT) (T-okres próbkowania) powstały poprzez próbkowanie ciągłego sygnału X(t) z częstotliwością f_p , to możemy dokonać odtworzenia sygnału ciągłego na podstawie próbek jeżeli częstot. Próbkowania była większa od podwojonej maksymalnej częstotliw. sygnału X(t) tzn f_p>2f_M Minimalna częstot. próbkowania przy której można jeszcze odtworzyć sygnał X(t) tzn f_p=f_M nazywa się czestotl. Nyquista. Odpowiadający jej okres T=1/f_p nazywa się przedziałem Nyquista

Def. transmitancji syst. DLS : skrót Z.W.P. - przy Zerowych Warunkach Początkowych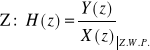
       

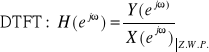
System DLS rzędu N

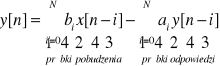
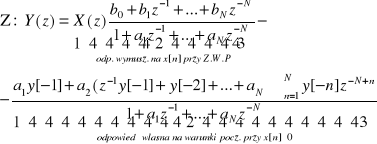
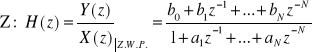
Równoważne spos.opisu sys.DLS na podst.transmitancji H(z): -równanie różnicowe; -odpowiedź impulsowa h[n] -rozkład zer i biegunów, -charakterystyki częstotliwościowe -schemat blokowy Kwantyzator (kwantyzer)-nazywamy ukł. przyporzą-cym próbkom, których wartości należą do zbioru ciągłego liczb rzeczywistych dyskretne wartości (poziomy). Zbiór dyskretnych wartości nazywamy poziomami kwantowania N bitowym kwantyzerze mamy 2^N poziomów kwantowania. Δ- krok kwantowania, δ - moc szumu; B - liczba bitów w B+1 bitowym słowie, rozdzielczość konwertera; 2^B+1 - liczba poziomów kwantowania; SNR - odstęp syg/szum

SNR=6B-1,25 ;
;

DTFT:
;
;

Zastosow: 1: szukanie widma sygnału 2: znajdowanie char. czasowych systemów dyskretnych

Wnioski: 1: Char. amp-faz syst. stabilnego, która stanowi transformatę F odpow. ipuls. jest zawsze zbieżna 2: bezwzględna sumowalność ciągu x[n] jest dostatecznym warun. ist. jego transfor.F

Def. systemu stabil:
Def. syst. przyczynow: h[n]=0, dla n<0

IDTFT: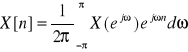

Wzorki różne: 

Niektóre pary tansfor.F - DTFT:

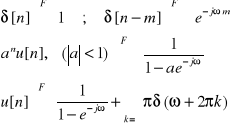
Niektóre pary tansfor.Z :

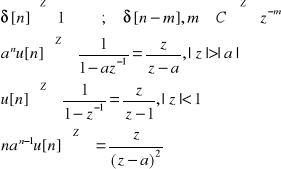
Właściwości transfor. Z: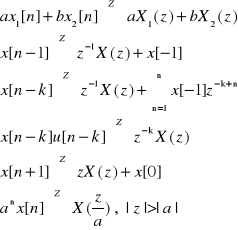

Przyczynowość ciągu polega na tym, że próbki ciągu dla n<0 mają wartość 0 ;

Stabilność ciągu polega na tym, że jego bieguny leżą wewnątrz okręgu jednostkowego. Jeżeli pobudzamy ukł.skończonym ciągiem oi w wyniku dostajemy ciąg o skończonej długości, to wtedy sys.jest stabilny.

Wzory na charakt.częstotli:

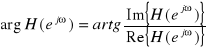
Rząd sys.DLS to liczba biegunów jego transmitancji lub maks.wart. opóźnienia wyst.w układzie; System FIR - sys.o skończ.odp.impulsowej

System IIR - sys.o nieskoń. odpow. impulsowej;

DTF : przekształcenie wyliczone dla ciągów o skończonej długości, używa się do reprezentacji widmowej sygnałów dyskretnych:
dla k=0,1...N-1,

Zastosow: DSP, gdzie nie można obliczyć DTFT, przy obliczaniu transformat w komputerach ;

IDFT:
dla n=0,1...N-1,

Związek DTF i IDTF   X[k]=X(ejω)przy ω=2πk/N= X(z)przy z= ej2πk/N=W_N^--K

Energia sygnału
;
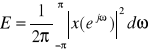
ener. liczona w dziedz t ma taką samą wart. jak energia licz.w dziedz.f

;

---