Bogdan Wilczyński

Zakład Mechaniki Technicznej

Wydział Mechaniczny

Politechnika Koszalińska

OGÓLNE ZASADY DYNAMIKI

1) Zasada pędu

2) Zasada zachowania pędu

3) Zasada zmienności energii kinetycznej (zasada pracy)

4) Zasada zachowania energii mechanicznej

5) Zasada zmienności momentu pędu (zasada krętu)

6) Zasada zachowania krętu

Zasada pędu

P.m. o masie m porusza się pod działaniem siły P. W chwili t1 ma prędkość v1, a w chwili t2 ma prędkość v2 (rys.).

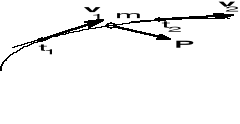
Zasadę pędu wyprowadza się z II prawa Newtona:

gdzie, mv jest pędem p.m., a Pdt jest impulsem (popędem) elementarnym siły.

Całkując obustronnie ostatni związek otrzymujemy:

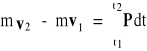
gdzie

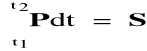
jest impulsem całkowitym siły P.

Przyrost geometryczny pędu p.m. między położniem początkowym w chwili t1, a położeniem początkowym w chwili t2 poruszającego się pod działaniem danej siły P jest równy impulsowi tej siły.

Przykład

Na p.m. o ciężarze Q poruszający się wzdłuż chropowatej równi pochyłej nachylonej pod kątem do poziomu działa stała siła F równoległa do równi. Obliczyć czas po którym prędkość początkowa v osiągnie wartość v1. Współczynnik tarcia dany.

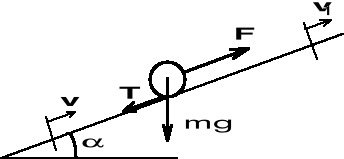
Wypadkowa P wszystkich sił działających na punkt materialnywynosi

P = F - mgcosa - mgsina = const

gdyż

T = N = mgcosa

Z zasady pędu mamy:

Stąd:

Zasada zachowania pędu

Jeśli P = 0, to:

mv = const.

Zasada zmienności energii kinetycznej (zasada pracy)

P.m. poruszający się pod działaniem siły P ma w położeniu początkowym (1) prędkość v1, a w położeniu końcowym (2) prędkość v2.

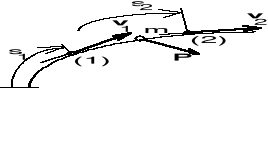
Przyrost energii kinetycznej p.m. na pewnym przemieszczeniu równa się pracy siły P na tym przemieszczeniu.

gdzie:
, L - praca siły P na odcinku (1) - (2).

Definicja pracy. Praca elementarna - iloczyn skalarny wektora siły P i wektora przemieszczenia elementarnego ds.

dL = Pds.

Praca siły na skończonym przemieszczeniu od położenia (1) do położenia (2):

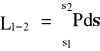
Praca siły w układzie współrzędnych naturalnych

Praca siły w układzie współrzędnych prostokątnych (płaskim)

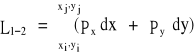
Przykłady obliczania pracy.

Praca siły sprężystej (k - sztywność sprężyny).

Mamy sprężynę śrubową zamocowaną na jednym końcu, na drugim zaś obciążoną (np. siłą rozciaganą) P. Siłą ta wywoła w sprężynie reakcję zwróconą przeciwnie. Zakładając, że przyłożona siła wydłuża sprężynę o wielkość obliczyć prace tej reakcji. Zakładamy,że siła w sprężynie jest wprost proporcjonalna do wydłużenia sprężyny, tj. F = kx.

Praca elementarna (jest ujemna, bo siła jest skierowana przeciwnie do kierunku przemieszczenia końca sprężyny) wynosi

dL = - Fdx = - kxdx

Po scałkowaniu

.

Praca siły ciężkości.

P.m. o masie m jest umieszczony w jednorodnym polu przyciągania Ziemi. Na punkt działa siła ciężkości mg (rys.). Obliczymy pracę, jaką wykona siła ciężkości przy przemieszczeniu punktu z położenia (1) do położenia (2).

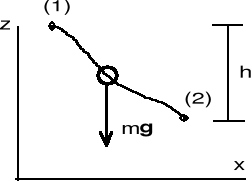
Praca elementarna:

dL = - Py dz = -mgdz

.

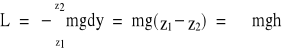
gdzie h = (z1-z2) jest różnicą poziomów położenia początkowego i końcowego, a znak + odnosi się do przypadku, gdy położenie (1) znajduje się powyżej położenia (2), natomiast znak - gdy odwrotnie.

Praca siły ciężkości po torze zamkniętym:

Z powyższego wzoru wynika, że praca siły ciężkości nie zależy od kształtu toru, po którym się porusza p. m., a zalezy jedynie od różnicy poziomów położenia początkowego i końcowego.

Drugi wniosek: praca po torze zamkniętym jest równa zeru.

L = 0 bo, L1-2 + L2-1 = mgh - mgh = 0.

Zasada zachowania energii mechanicznej

W polu potencjalnym (sił potencjalnych) suma energii kinetycznej i potencjalnej p.m. jest w każdym położeniu wielkością stałą.

E + U = const, lub

E1 + U1 = E2 + U2,

gdzie:

E - energia kinetyczna p.m.,

U - energia potencjalna p.m..

Definicja. Pole potencjane (pole sił potencjalnych) - pole sił zależnych tylko od położenia punktu.

Przykłady pól potencjalnych:

- pole siły cięźkości,

- pole siły sprężystej,

- pole siły centralnej.

Uwaga! Pole sił tarcia nie jest polem potencjalnym.

Energia potencjalna w jednorodnym polu grawitacyjnym

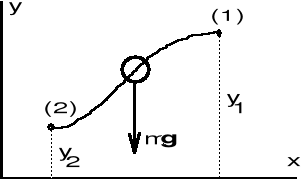
U = Uo + mg(y1 - y2 ) = Uo + mgh

gdzie: Uo - stała całkowania, możemy przyjąć wartośc zerową.

Energia potencjalna siły spręźystej (o własnościach liniowych):

gdzie: k - sztywność sprężyny, a jest wydłużeniem sprężyny.

Zasada krętu (zmienności momentu pędu)

Definicja krętu.

Krętem p.m. (momentem pędu) względem punktu O nazywamy wektor otrzymany w wyniku mnożenia wektorowego wektora-promienia r i wektora pędu p = mv.

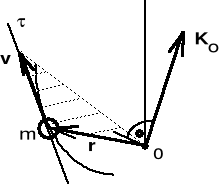
lub

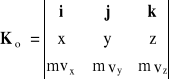
gdzie: i, j, k - wersory na osiach układu xyz, x, y, z - współrzędne p.m., mvx, mvy, mvz - składowe wektora pędu.

Można wykazać, źe zachodzi następujący związek (zasada krętu):

Pochodna względem czasu krętu p.m. względem dowolnie obranego punktu O równa się momentowi siły P działającej na ten p.m. względem tego samego punktu O.

Przykład. Zasadę krętu wykorzystać do wyprowadzenia równania ruchu wahadła matematycznego (m,l dane).

Wypadkowa sił działających na p.m.

P = mg + N

Składowe wektora siły P:

P = (mg - Ncos, - Nsin).

Stąd:

P = (mg-Ncos) i + (-Nsin) j.

Ponieważ:

r = xi + yj = lcos i + lsin j, to

v = dr/dt = - lsin d/dt i, + lcos d/dt j.

Wykorzystując zapis wyznacznikowy mamy:

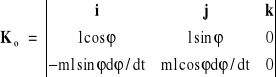
Również, wykorzystując zapis wyznacznikowy obliczamy moment siły P względem punktu zawieszenia wahadła O:

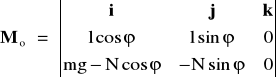
Po zróżniczkowaniu Ko względem czasu t i uporządkowaniu równania zasady krętu otrzymujemy:

.

Zakładając małe wahania wahadła matematycznego (czyli sin ) otrzymujemy ostatecznie równanie ruchu wahadła:

Zasada zachowania krętu

Jeśli M = 0, to K = const.

Siła bezwładności. Zasada d'Alemberte'a

Def. Siła bezwładności B jest do siła fikcyjna wyznaczana z zależności

B = - ma

gdzie: m - masa p.m., a - wektor przyspieszenia tego punktu.

Przykłady sił bezwładności pokazuje poniższy rysunek: a) w ruchu prostoliniowym, b) składowa normalna siły bezwładności w ruchu wahadła matematycznego, c) ruch po dowolnym torze krzywoliniowym (styczna B_τ i normalna B_n siła bezwładności; ta ostatnia nazywana jest siłą odśrodkową)

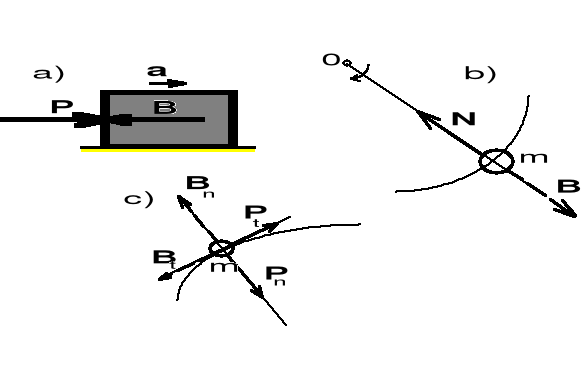
Zasada d”Alemberta

W każdej chwili wypadkowa sił czynnych (rzeczywistych) równoważy się z siłą bezwładności tego punktu.

P + B = 0

B. Wilczyński Mechanika ogólna

---